2012年10月4日,云南省彝良县发生特大泥石流,一汽车停在小山坡底,突然司机发现在距坡底240 m的山坡处泥石流以8 m/s的初速度、0.4 m/s2的加速度匀加速倾泻而下,假设泥石流到达坡底后速率不变,在水平地面上做匀速直线运动。已知司机的反应时间为1 s,汽车启动后以0.5 m/s2的加速度一直做匀加速直线运动。试分析汽车能否安全脱离?
如图所示,倾角θ=30°,宽度L=1m的足够长的U形平行光滑金属导轨,固定在磁感强度B=1T,范围充分大的匀强磁场中,磁场方向与导轨平面垂直.用平行于导轨,功率恒为6W的牵引力F牵引一根质量m=0.2kg,电阻R=1Ω放在导轨上的金属棒ab,由静止开始沿导轨向上移动(ab始终与导轨接触良好且垂直),当ab棒移动2.8m时获得稳定速度,在此过程中,金属棒产生的热量为5.8J(不计导轨电阻及一切摩擦,取g=10m/s2),求:
(1)ab棒的稳定速度;
(2)ab棒从静止开始达到稳定速度所需时间.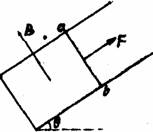
一个质量m=0.1kg的正方形金属框总电阻R=0.5Ω,金属框放在表面绝缘且光滑的斜面顶端(金属框上边与AA′重合),自静止开始沿斜面下滑,下滑过程中穿过一段边界与斜面底边BB′平行、宽度为d的匀强磁场后滑至斜面底端(金属框下边与BB′重合),设金属框在下滑过程中的速度为v,与此对应的位移为s,那么v2―s图象如图所示,已知匀强磁场方向垂直斜面向上,g=10m/s2。
(1)根据v2―s图象所提供的信息,计算出斜面倾角θ和匀强磁场宽度d.
(2)金属框从进入磁场到穿出磁场所用的时间是多少?
(3)匀强磁场的磁感应强度多大。
在互相垂直的匀强磁场和匀强电场中固定放置一光滑的绝缘斜面,其倾角为θ,设斜面足够长,磁场的磁感应强度为B,方向垂直纸面向外,电场方向竖直向上,如图所示。一质量为m带电量为q的小球静止放在斜面的最高点A,小球对斜面的压力恰好为零。在释放小球的同时,将电场方向迅速改为竖直向下,电场强度大小不变.
(1)小球沿斜面下滑的速度v为多大时,小球对斜面的正压力再次为零?
(2)小球从释放到离开斜面一共历时多少?
如图(a)所示,在以直角坐标系xOy的坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度大小为B、方向垂直xOy所在平面的匀强磁场。一带电粒子由磁场边界与x轴的交点A处,以速度v0沿x轴负方向射入磁场,粒子恰好能从磁场边界与y轴的交点C处,沿y轴正方向飞出磁场,不计带电粒子所受重力。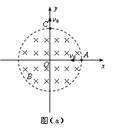
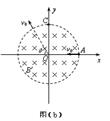
(1)求粒子的荷质比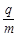 。(要求画出粒子在磁场中运动轨迹的示意图)
。(要求画出粒子在磁场中运动轨迹的示意图)
(2)若磁场的方向和所在空间的范围不变,而磁感应强度的大小变为B′,该粒子仍从A处以相同的速度射入磁场,粒子飞出磁场时速度的方向相对于入射方向改变了θ角,如图(b)所示,求磁感应强度B′的大小。(要求画出粒子在磁场中运动轨迹的示意图)
如图所示,在两平行边界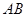 、
、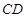 的狭长区域内,分布有磁感应强度为
的狭长区域内,分布有磁感应强度为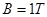 而方向垂直纸面向外的匀强磁场,磁场区域宽度为
而方向垂直纸面向外的匀强磁场,磁场区域宽度为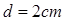 。一带正电的粒子,质量为
。一带正电的粒子,质量为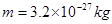 ,带电量为
,带电量为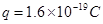 ,以速率
,以速率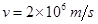 从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求:
从左边界的O处斜向上射入磁场,粒子刚好从另一边界垂直射出,求: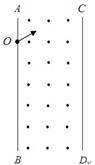
(1)请画出带电粒子在磁场中运动的运动轨迹
(2)带电粒子在磁场中的轨道半径r为多大?
(3)带电粒子在磁场中的运动时间t是多少?(此小题结果保留三位有效数字)