已知一艘轮船载重量是
吨，容积是
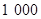立方米．现有甲、乙两种货待装，甲种货物每吨体积是
立方米，乙种货物每吨体积是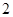
立方米，求怎么样货才能最大限度的利用船的载重量和体积？如果设装甲种货物
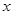吨，乙种货物
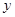吨，根据题意列方程组得（ ）
A． |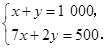
B． |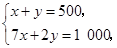
C． |
D． |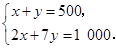
如下图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，沿AC方向匀速运动到终点C，动点Q从点C出发，沿CB方向匀速运动到终点B．已知P，Q两点同时出发，并同时到达终点．连结MP，MQ，PQ，在整个运动过程中，△MPQ的面积大小变化情况是（）.
A．一直增大 B．一直减小C．先减小后增大D．先增大后减小
二次函数
的图象如下图，若方程
有实数根，则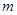
的最大值为（）. 
| A．-3 | B．3 | C．-6 | D．0 |
如图，小圆经过大圆的圆心O，且∠ADB=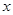
，∠ACB=
，则与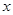之间的关系是（）.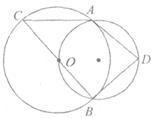
A． |
B． |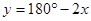
C． |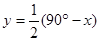
D． |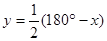
在原点为O的平面直角坐标系中，⊙O的半径为l，则直线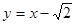
与⊙O的位置关系是（）.
| A．相离 | B．相切 | C．相交 | D．以上三种情况都有可能 |
如图，AB∥CD，下列结论中正确的是（）.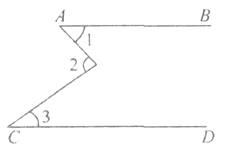
| A．∠l+∠2+∠3=180° | B．∠l+∠2+∠3="360°" |
| C．∠l+∠3=2∠2 | D．∠l+∠3=∠2 |