已知函数 在R是奇函数,且当
在R是奇函数,且当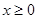 时,
时, ,则
,则 时,
时, 的解析式为_______________
的解析式为_______________
给出下列四个命题:
①函数f(x)=lnx-2+x在区间(1 , e)上存在零点;
②若m≥-1,则函数 的值域为R;
的值域为R;
③若 ,则函数y=f(x)在x=x0处取得极值;
,则函数y=f(x)在x=x0处取得极值;
④“a =1”是“函数 在定义域上是奇函数”的充分不必要条件。
在定义域上是奇函数”的充分不必要条件。
其中正确的是。
对正整数 ,设曲线
,设曲线 在
在 处的切线与
处的切线与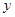 轴交点的纵坐标为
轴交点的纵坐标为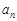 ,则数列
,则数列 的前
的前 项和的公式是。
项和的公式是。
椭圆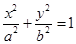 (a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为.
(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为.
如右图,抛物线C: (p>0)的焦点为F,A为C上的点,以F为圆心,
(p>0)的焦点为F,A为C上的点,以F为圆心,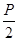 为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠
为半径的圆与线段AF的交点为B,∠AFx=60°,A在y轴上的射影为N,则∠ =.
=.
设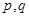 是两个命题
是两个命题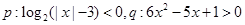 ,
,
则 是
是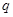 的条件。 (填“充分而不必要”、“ 必要而不充分”、“ 充分必要 ”、“ 既不充分也不必要”中的一个)
的条件。 (填“充分而不必要”、“ 必要而不充分”、“ 充分必要 ”、“ 既不充分也不必要”中的一个)