如图所示，两条公路互相垂直，在南北方向的公路上，汽车甲以8m/s的速度从北向南匀速行驶；在东西方向的公路上，汽车乙以6m/s的速度，从东向西匀速行驶。当甲行至交叉路口时，乙行至路口以东100m处。问此后何时两车间距离最近？这个距离是多少？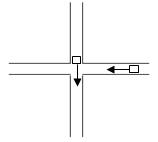
如图，ABC三个木块的质量均为m。置于光滑的水平面上，BC之间有一轻质弹簧，弹簧的两端与木块接触可不固连，将弹簧压紧到不能再压缩时用细线把BC紧连，是弹簧不能伸展，以至于BC可视为一个整体，现A以初速
沿BC的连线方向朝B运动，与B相碰并粘合在一起，以后细线突然断开，弹簧伸展，从而使C与A，B分离，已知C离开弹簧后的速度恰为，求弹簧释放的势能。
一半圆柱形透明物体横截面如图所示，地面AOB镀银，（图中粗线），O表示半圆截面的圆心，一束光线在横截面内从M点的入射，经过AB面反射后从N点射出，已知光线在M点的入射角为30
，
MOA=60，NOB=30。求
（i）光线在M点的折射角
（ii）透明物体的折射率
如图，一上端开口，下端封闭的细长玻璃管，下部有长l1=66cm的水银柱，中间封有长l2=6．6cm的空气柱，上部有长l3=44cm的水银柱，此时水银面恰好与管口平齐。已知大气压强为Po=76cmHg。如果使玻璃管绕低端在竖直平面内缓慢地转动一周，求在开口向下和转回到原来位置时管中空气柱的长度。封入的气体可视为理想气体，在转动过程中没有发生漏气。
如图，在区域I（0≤x≤d）和区域II（d≤x≤2d）内分别存在匀强磁场，磁感应强度大小分别为B和2B，方向相反，且都垂直于Oxy平面。一质量为m、带电荷量q（q＞0）的粒子a于某时刻从y轴上的P点射入区域I，其速度方向沿x轴正向。已知a在离开区域I时，速度方向与x轴正方向的夹角为30°；此时，另一质量和电荷量均与a相同的粒子b也从p点沿x轴正向射入区域I，其速度大小是a的1/3。不计重力和两粒子之间的相互作用力。求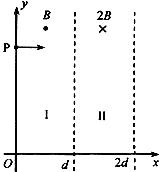
（1）粒子a射入区域I时速度的大小；
（2）当a离开区域II时，a、b两粒子的y坐标之差。
甲乙两辆汽车都从静止出发做加速直线运动，加速度方向一直不变。在第一段时间间隔内，两辆汽车的加速度大小不变，汽车乙的加速度大小是甲的两倍；在接下来的相同时间间隔内，汽车甲的加速度大小增加为原来的两倍，汽车乙的加速度大小减小为原来的一半。求甲乙两车各自在这两段时间间隔内走过的总路程之比。