已知sin(3π-α)=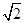 cos
cos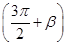 ,cos(π-α)=
,cos(π-α)=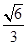 ·cos(π+β),且0<α<π,0<β<π,求sinα和cosβ.
·cos(π+β),且0<α<π,0<β<π,求sinα和cosβ.
(本小题14分)用分析法证明: 已知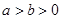 ,求证
,求证
(本小题14分)已知函数 ,当
,当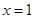 时,有极大值
时,有极大值 ;
;
(1)求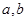 的值;(2)求函数
的值;(2)求函数 的极小值。
的极小值。
已知圆 的圆心在直线
的圆心在直线 上,且圆
上,且圆 与
与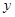 轴相切,若圆
轴相切,若圆 截直线
截直线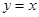 得弦长为
得弦长为 ,求圆
,求圆 的方程.
的方程.
(本小题满分12分)
某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别是0.3、0.2、0.1、0.4,求:
(1)他乘火车或乘飞机去的概率;
(2)他不乘轮船去的概率;
(3)如果他乘交通工具去的概率为0.5,请问他有可能是乘何种交通工具去的?
某化肥厂有甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量(单位:kg),分别记录抽查数据如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种方法?
(2)试计算甲、乙两个车间产品重量的平均数与方差,并说明哪个车间产品较稳定。