有甲、乙、丙三种规格的钢条,已知甲种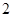 根,乙种
根,乙种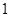 根,丙种
根,丙种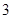 根,共长
根,共长 米;甲种
米;甲种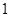 根,乙种
根,乙种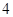 根,丙种
根,丙种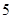 根共长
根共长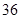 米,问甲
米,问甲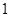 根,乙
根,乙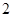 根,丙
根,丙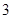 根共长多少?
根共长多少?
如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以 OA为半径的⊙O经过点D。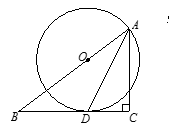
(1)求证: BC是⊙O切线;
(2)若BD="5," DC="3," 求AC的长。
如图,A(-1,0),B(2,-3)两点都在一次函数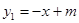 与二次函数
与二次函数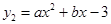 的图象上.
的图象上.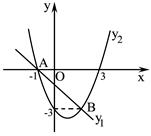
(1)求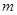 和
和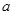 ,
,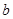 的值;
的值;
(2)请直接写出当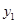 >
>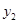 时,自变量
时,自变量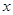 的取值范围.
的取值范围.
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.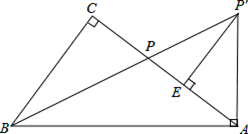
(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当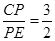 ,,BP′=5
,,BP′=5 时,求线段AB的长.
时,求线段AB的长.
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元.则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
如图,在平行四边形ABCD中,过点A作AE垂直BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B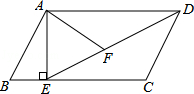
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6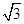 ,AF=4
,AF=4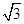 ,求AE的长.
,求AE的长.