(本小题满分13分)已知 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时
时 ;
;
(1)求函数 的表达式;
的表达式;
(2)画出其大致图像并指出其单调区间.
(3)若函数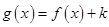 -1有三个零点,求K的取值范围;
-1有三个零点,求K的取值范围;
(本小题满分12分)
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,已知
,已知
(Ⅰ)求 的值;
的值;
(Ⅱ) 求
求 的面积
的面积
(本小题满分15分)
设函数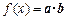 ,其中向量
,其中向量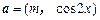 ,
,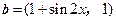 ,
,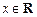 ,且
,且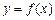 的图象经过点
的图象经过点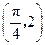 .
.
(Ⅰ)求实数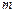 的值;
的值;
(Ⅱ)求函数 的最小值及此时
的最小值及此时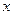 值的集合.
值的集合.
(本小题满分15分)
已知向量 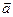 =(cos
=(cos ,sin
,sin ),
),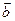 =(cos
=(cos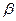 ,sin
,sin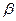 ),|
),|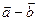 |=
|=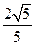 .
.
(1)求cos( -
-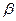 )的值;
)的值;
(2)若0< <
<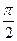 ,-
,-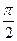 <
<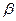 <0,且sin
<0,且sin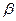 =-
=-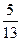 ,求sin
,求sin 的值
的值
(本小题满分14分)
已知
(1)求 ;
;
(2)若 与
与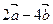 平行,求
平行,求 的值;
的值;
(3)若 与
与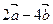 的夹角是钝角,求实数
的夹角是钝角,求实数 的取值范围.
的取值范围.
(本小题满分14分)
△ABC中,角A、B、C的对边分别为a、b、c,
且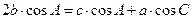 ,
,
(1)求角A的大小;
(2)若 ,求△ABC的面积.
,求△ABC的面积.