(本小题满分13分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度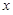 (单位:cm)满足关系:
(单位:cm)满足关系: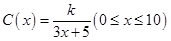 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设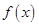 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求 的值及
的值及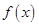 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用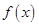 达到最小,并求最小值.
达到最小,并求最小值.
(本题满分13分)已知数列{an}的前n项和为Sn,且an=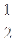 (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设 ,求数列
,求数列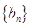 的前n项和Bn;
的前n项和Bn;
已知△ABC的内角A,B,C所对的边分别为a,b,c.它的外接圆半径为6. ∠B,∠C和△ABC的面积S满足条件: 且
且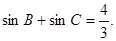
(1)求
(2)求△ABC面积S的最大值.
(本小题满分12分)在 中,
中, ,
, .
.
(1)求角 的大小;
的大小;
(2)若 最大边的边长为
最大边的边长为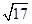 ,求最小边的边长.
,求最小边的边长.
已知数列 满足
满足
 是
是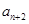 与
与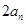 的等差中项
的等差中项
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(本小题满分13分)已知函数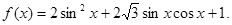 求:
求:
(1)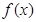 的最小正周期;(2)
的最小正周期;(2)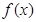 的单调递增区间;(3)
的单调递增区间;(3)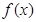 在
在 上的最值.
上的最值.