已知椭圆 的左右焦点
的左右焦点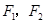 ,其离心率为
,其离心率为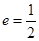 ,点
,点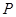 为椭圆上的一个动点,
为椭圆上的一个动点,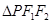 内切圆面积的最大值为
内切圆面积的最大值为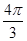 .
.
(1)求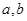 的值;
的值;
(2)若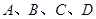 是椭圆上不重合的四个点,且满足
是椭圆上不重合的四个点,且满足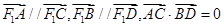 ,求
,求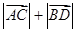 的取值范围.
的取值范围.
已知公比不为1的等比数列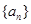 的前
的前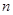 项和为
项和为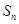 ,
,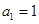 ,且
,且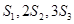 成等差数列.
成等差数列.
(1)求数列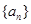 的通项公式;
的通项公式;
(2)设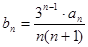 ,求数列
,求数列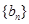 的前
的前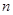 项和
项和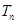 .
.
已知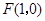 ,直线
,直线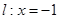 ,
,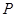 为平面上的动点,过点
为平面上的动点,过点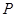 作
作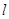 的垂线,垂足为点
的垂线,垂足为点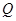 ,且
,且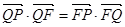 .
.
(1)求动点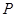 的轨迹曲线
的轨迹曲线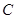 的方程;
的方程;
(2)设动直线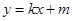 与曲线
与曲线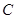 相切于点
相切于点 ,且与直线
,且与直线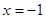 相交于点
相交于点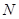 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点 ,使得以
,使得以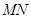 为直径的圆恒过此定点
为直径的圆恒过此定点 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
某工厂在试验阶段大量生产一种零件,这种零件有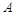 、
、 两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为
两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为 .按质量检验规定:两项技术指标都达标的零件为合格品.
.按质量检验规定:两项技术指标都达标的零件为合格品.
(1)求一个零件经过检测为合格品的概率是多少?
(2)任意依次抽取该种零件4个,设 表示其中合格品的个数,求
表示其中合格品的个数,求 的分布列及数学期望
的分布列及数学期望 .
.
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA, .
.
(1)证明:平面PQC⊥平面DCQ;
(2)求二面角Q—BP—C的余弦值.
数列 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列.
(1)求 的值;
的值;
(2)求 的通项公式.
的通项公式.