.已知函数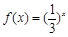 , 其反函数为
, 其反函数为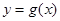
(1) 若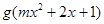 的定义域为
的定义域为 ,求实数
,求实数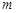 的取值范围;
的取值范围;
(2) 当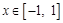 时,求函数
时,求函数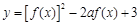 的最小值
的最小值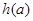 ;
;
(3) 是否存在实数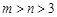 ,使得函数
,使得函数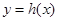 的定义域为
的定义域为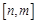 ,值域为
,值域为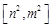 ,若存在,求出
,若存在,求出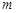 、
、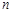 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.
如图,菱形ABCD所在平面与矩形ACEF所在平面相互垂直,点M是线段EF的中点。(1)求证:AM // 平面BDE(2)当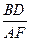 为何值时,平面DEF
为何值时,平面DEF 平面BEF?并证明你的结论。
平面BEF?并证明你的结论。
已知向量 ,
, .(1)当
.(1)当 ,且
,且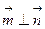 时,求
时,求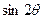 的值;(2)当
的值;(2)当 ,且
,且 ∥
∥ 时,求
时,求 的值.
的值.
已知函数f(x)=ax2+ax和g(x)=x-a,其中aÎR且a¹0.
(1)若函数f(x)与g(x)的图像的一个公共点恰好在x轴上,求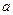 的值;
的值;
(2)若函数f(x)与g(x)图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的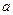 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
(3)若p和q是方程f(x)=g(x)的两根,且满足0<p<q<,证明:当xÎ(0,p)时,g(x)<f(x)<p-a..
某地政府为科技兴市,欲在如图所示的矩形ABCD的非农业用地中规划出一个高科技工业园区(如图中阴影部分),形状为直角梯形QPRE(线段EQ和RP为两个底边),已知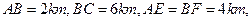 其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
其中AF是以A为顶点、AD为对称轴的抛物线段.试求该高科技工业园区的最大面积.
如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点 ,顶点
,顶点 在
在 轴上,点
轴上,点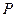 为线段
为线段 的中点(1)求
的中点(1)求 边所在直线方程;
边所在直线方程;
(2) 为直角三角形
为直角三角形 外接圆的圆心,求圆
外接圆的圆心,求圆 的方程;(3)求过(-2,4)与圆相切的直线方程.
的方程;(3)求过(-2,4)与圆相切的直线方程.