(本小题满分10分)选修41:几何证明选讲
如图,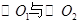 相交于A、B两点,AB是
相交于A、B两点,AB是 的直径,过A点作
的直径,过A点作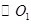 的切线交
的切线交 于点E,并与BO1的延长线交于点P,PB分别与
于点E,并与BO1的延长线交于点P,PB分别与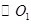 、
、 交于C,D两点.
交于C,D两点.
求证:(1)PA·PD=PE·PC; (2)AD=AE.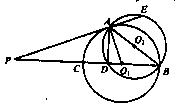
设数列 满足
满足 .
.
(Ⅰ)求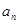 ;
;
(Ⅱ)设 ,
, ,求证:数列
,求证:数列 中
中 最小.
最小.
(本小题满分15分)
对于函数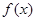 ,若存在
,若存在 ,使
,使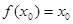 成立,则称
成立,则称 为
为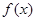 的一个不动点.
的一个不动点.
设函数 (
( ).
).
(Ⅰ)当 ,
,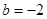 时,求
时,求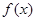 的不动点;
的不动点;
(Ⅱ)设函数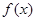 的对称轴为直线
的对称轴为直线 ,
, 为
为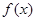 的不动点,当
的不动点,当 时,求证:
时,求证: .
.
(本小题满分15分)
已知椭圆 :
: .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)设直线 与椭圆
与椭圆 交于不同两点
交于不同两点 ,若点
,若点 满足
满足 ,求实数
,求实数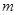 的值.
的值.
(本小题满分15分)等差数列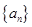 中,
中, ,
, .
.
(Ⅰ)求数列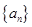 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列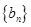 的前
的前 项和
项和 .
.
(本小题满分14分)
对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称 为
为 的一个不动点.
的一个不动点.
设函数 (
( ).
).
(Ⅰ)当 ,
, 时,求
时,求 的不动点;
的不动点;
(Ⅱ)若 有两个相异的不动点
有两个相异的不动点 .
.
(i)当 时,设
时,设 的对称轴为直线
的对称轴为直线 ,求证:
,求证: ;
;
(ii)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.