一批货物要运往某地，货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车情况如下表：
| |
第一次 |
第二次 |
| 甲种货车辆数(单位:辆) |
2 |
5 |
| 乙种货车辆数(单位：辆) |
3 |
6 |
| 累计运货吨数(单位：吨) |
15.5 |
35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货物，如果按每吨付运费30元计算，问：货主应付运费多少元？
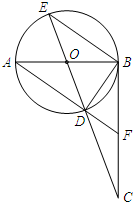
已知
是方程
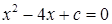的一个根，求方程的另一个根及c的值。
当
时，求代数式 
的值。
解一元二次方程:
如图，抛物线y=ax2+2ax+c（a≠0）与y轴交于点C（0，4），与x轴交于点A（﹣4，0）和B．
（1）求该抛物线的解析式；
（2）点Q是线段AB上的动点，过点Q作QE∥AC，交BC于点E，连接CQ．当△CEQ的面积最大时，求点Q的坐标；
（3）平行于x轴的动直线l与该抛物线交于点P，与直线AC交于点F，点D的坐标为（﹣2，0）．问是否有直线l，使△ODF是等腰三角形？若存在，请求出点F的坐标；若不存在，请说明理由．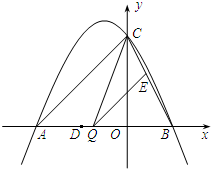
如图，AB是⊙O的直径，BC切⊙O于点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．
（1）试判断∠CBD与∠CEB是否相等，并证明你的结论；
（2）求证：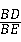
=
；
（3）若BC=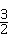
AB，求tan∠CDF的值．