如图,抛物线y=ax2+2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A(﹣4,0)和B.
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CEQ的面积最大时,求点Q的坐标;
(3)平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(﹣2,0).问是否有直线l,使△ODF是等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由.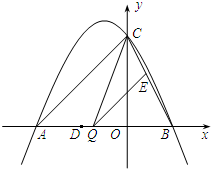
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
求证:D是弧AE的中点;
求证:∠DAO=∠B+∠BAD;
若
 ,且AC=4,求CF的长.
,且AC=4,求CF的长.
两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=2.
固定△ABC不动,将△DEF进行如下操作:如图(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,它的面积是否变化,如果不变请求出其面积.如果变化,说明理由.
如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由
如图(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,
使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出 的值.
的值.


某厂家新开发一种摩托车如图所示,它的大灯A射出的光线AB、AC与地面MN的夹角分别为8°和10°,大灯A与地面距离1 m.该车大灯照亮地面的宽度BC约是多少?
一般正常人从发现危险到做出刹车动作的反应时间是0.2 s,从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离,某人以60km/h的速度驾驶该车,突然遇到危险情况,立即刹车直到摩托车停止,在这过程中刹车距离是
 m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据:
m,请判断该车大灯的设计是否能满足最小安全距离的要求,请说明理由.(参考数据: ,
, ,
, ,
, )
)
已知:如图,一次函数 的图象与反比例函数
的图象与反比例函数 (
( )的图象交于点
)的图象交于点 .
. 轴于点
轴于点 ,
, 轴于点
轴于点 .一次函数的图象分别交
.一次函数的图象分别交 轴、
轴、 轴于点
轴于点 、点
、点 ,
,  ,且tan∠PDB=
,且tan∠PDB= .
.
求点
 的坐标;
的坐标;求一次函数与反比例函数的解析式;
根据图象写出当
 取何值时,一次函数的值小于反比例函数的值?
取何值时,一次函数的值小于反比例函数的值?
小明和小颖做掷骰子的游戏,规则如下:①游 戏前,每人选一个数字;②每次同时掷两枚均匀骰子;③如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.用列表法或树状图列出同时掷两枚均匀骰子所有可能出现的结果:
小明选的数字是5,小颖选的数字是8.如果你也加入游戏,你会选什么数字,使自己获胜的概率比他们大?请说明理由.