△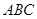 中,
中,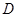 为
为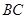 边的中点,过
边的中点,过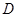 点分别作
点分别作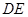 ∥
∥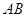 交
交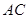 于点
于点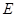 ,
,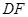 ∥
∥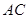 交
交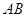 于点
于点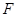 .(本题10分)
.(本题10分)
(1)证明:△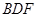 ≌△
≌△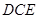 ;
;
(2)如果给△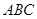 添加一个条件,使四边形
添加一个条件,使四边形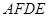 成为菱形,则该条件是 ;
成为菱形,则该条件是 ;
如果给△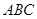 添加一个条件,使四边形
添加一个条件,使四边形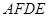 成为矩形,则该条件是 .
成为矩形,则该条件是 .
(均不再增添辅助线) 请选择一个结论进行证明.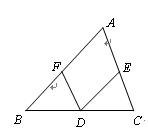
在数轴上表示下列各数:0,–2.5,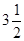 ,–2,+5,
,–2,+5, ,并比较它们的大小.
,并比较它们的大小.
如图1,正方形ABCD中,E、F分别在AD、DG上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
(1)求证:∠ABE=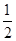 ∠BGE;
∠BGE;
(2)如图2,若AB=5,AE=2,求S△BEG;
(3)如图3,若E、F两点分别在AD、DC上运动,其它条件不变,试问:线段AE、EF、FC三者之间是否存在确定的数量关系?若存在,请写出它们之间的数量关系,并证明;若不存在,请说明理由.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交C于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
观察下列等式:
①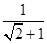 =
= 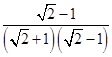 =
= 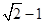 ;
;
②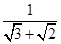 =
= 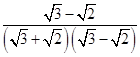 =
=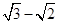 ;
;
③ =
= 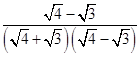 =
= 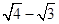 ;…
;…
回答下列问题:
(1)化简: = ;
= ;
(2)化简: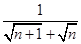 = (n为正整数);
= (n为正整数);
(3)利用上面所揭示的规律计算: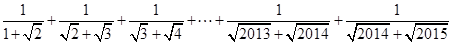 .
.
如图,AD是△ABC的中线,点E是AD的中点,点F是BE延长线与AC的交点,求 的值.
的值.