某学校办公楼前有一长为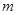 ,宽为
,宽为 的长方形空地,在中心位置留出一个半径为
的长方形空地,在中心位置留出一个半径为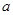 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.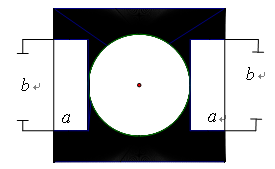
(1)用含字母和 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;
(2)当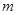 =4,
=4, =3,
=3,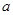 =1,
=1,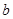 =2时,阴影部分面积是多少?(
=2时,阴影部分面积是多少?( 取3)
取3)
如图,某中学九年级数学兴趣小组测量校内旗杆AB的高度,在C点测得旗杆顶端A的仰角∠BCA=30°,向前走了20米到达D点,在D点测得旗杆顶端A的仰角∠BDA=60°,求旗杆AB的高度.(结果保留根号)
某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,三人中谁的得分最高?
解分式方程: .
.
(1)计算: ;
;
(2)解不等式 ,并将其解集表示在数轴上.
,并将其解集表示在数轴上.
(本题12分)如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,∠AOC的平分线交AB于点D,E为BC的中点,已知A(0,4)、C(5,0),二次函数 的图象经过A、C两点.
的图象经过A、C两点.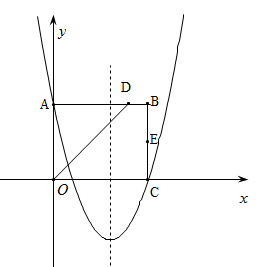

(1)求该二次函数的表达式;
(2)F、G分别为x轴、y轴上的动点,守卫顺次连结D、E、F、G构成四边形DEFG,求四边形DEFG周长的最小值;
(3)抛物线上是否存在点P,使△ODP的面积为12?若存在,求出点P的坐标;若不存在,请说明理由.