（本题12分）如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，∠AOC的平分线交AB于点D，E为BC的中点，已知A（0，4）、C（5，0），二次函数
的图象经过A、C两点．
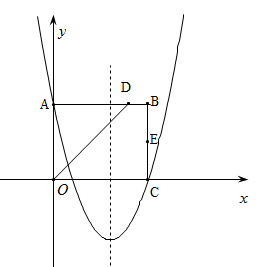
（1）求该二次函数的表达式；
（2）F、G分别为x轴、y轴上的动点，守卫顺次连结D、E、F、G构成四边形DEFG，求四边形DEFG周长的最小值；
（3）抛物线上是否存在点P，使△ODP的面积为12？若存在，求出点P的坐标；若不存在，请说明理由．
计算：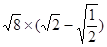
如图，二次函数
的图像交
轴于
，交
轴于
，过
画直线。
（1）求二次函数的解析式；
（2）点
在轴正半轴上，且
，求
的长；
（3）点
在二次函数图像上，以为圆心的圆与直线
相切，切点为
。
① 点在轴右侧，且
（点
与点
对应），求点的坐标；
② 若
的半径为
，求点的坐标。
邻边不相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形
中，若
，则平行四边形为1阶准菱形。
（1）判断与推理：
① 邻边长分别为2和3的平行四边形是__________阶准菱形；
② 小明为了剪去一个菱形，进行如下操作：如图2，把平行四边形沿着
折叠（点
在
上）使点
落在
边上的点
，得到四边形
，请证明四边形是菱形。
（2）操作、探究与计算：
① 已知平行四边形的邻边分别为1，
裁剪线的示意图，并在图形下方写出
的值；
② 已知平行四边形的邻边长分别为
，满足
，请写出平行四边形是几阶准菱形。
为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费。下表是该市民居民“一户一表”生活用水阶梯式计费价格表的部分信息：
（说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费）
已知小王家2012年4月用水20吨，交水费66元，5月份用水25吨，交水费91元。
（1）求a，b的值；
（2）随着夏天的到来，用水量将增加。为了节省开支。小王计划把6月份的水费控制在不超过家庭月收入的2%，若小王家的月收入为9200元，则小王家6月份最多能用水多少吨？
如图，
中，
是它的角平分线，
，
在
边上，
为直径的半圆
经过点
，交
于点
。
（1）求证：
是
的切线；
（2）已知
，的半径为4，求图中阴影部分的面积。