如图,在平面直角坐标系中。已知四边形 为菱形,且 .
(1)求过点 的反比例函数解析式;
(2)设直线 与(1)中所求函数图象相切,且与 轴, 轴的交点分别为 为坐标原点.求证: 的面积为定值.

如图, 中, ,边 在 轴上,反比例函数 的图象经过斜边 的中点 ,与 相交于点N, .
(1)求 的值;
(2)求直线 的解析式.
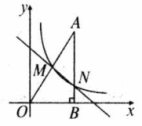
如图所示,在平面直角坐标系 中,一次函数 的图象 与函数 的图象(记为 交于点 ,过点 作 轴于点 ,且 ,点 在线段 上(不含端点),且 ,过点 作直线 轴,交 于点 ,交图象 于点 .
(1)求 的值,并且用含 的式子表示点 的横坐标;
(2)连接 ,记 的面积分别为 ,设 ,求 的最大值.

如图,正比例函数 的图象与反比例函数 的图象交于点 .在 中, ,点 坐标为 .
(1)求 的值;
(2)求 所在直线的解析式.

一场数学游戏在两个非常聪明的学生甲、乙之间进行.裁判先在黑板上写出下面的正整数 ,然后随意擦去一个数.接下来由乙、甲两人轮流擦去其中的一个数(即乙先擦去其中的一个数,然后甲再擦去一个数,如此轮流下去),若最后剩下的两个数互质,则判甲胜;否则,判乙胜.
按照这种游戏规则,求甲获胜的概率(用具体的数字作答).