如图所示,在平面直角坐标系 中,一次函数 的图象 与函数 的图象(记为 交于点 ,过点 作 轴于点 ,且 ,点 在线段 上(不含端点),且 ,过点 作直线 轴,交 于点 ,交图象 于点 .
(1)求 的值,并且用含 的式子表示点 的横坐标;
(2)连接 ,记 的面积分别为 ,设 ,求 的最大值.

先化简,再求值:
,其中  .
.
计算: .
如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.

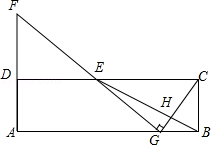
在矩形ABCD中,E为CD的中点,H为BE上的一点, ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
(1)求证: ;
(2)若∠CGF=90°,求 的值.
为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.