王大伯几年前承办了甲、乙两片荒山,各栽100棵杨梅树,成活98%,现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如拆线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲乙两山杨梅的产量总和;
(2)试通过计算说明,哪个山上的杨梅产量较稳定?
(本题满分12分)一名篮球运动员传球,球沿抛物线y=-x2+2x+4运行,传球时,球的出手点P的高度为1.8米,一名防守队员正好处在抛物线所在的平面内,他原地竖直起跳的最大高度为3.2米,
问:(1)球在下落过
 程中,防守队员原地竖直起跳后在到达最大高度时刚好将球断掉,那么传球时,两人相距多少米?
程中,防守队员原地竖直起跳后在到达最大高度时刚好将球断掉,那么传球时,两人相距多少米?(2)要使球在运行过程中不断防守队员断掉,且仍按抛物线y=-x2+2x+4运行,那么两人间的距离应在什么范围内?(结果保留
 根号)
根号)
学校为了美化校园环境,在一块长 米,宽
米,宽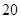 米的长方形空地上计划新建一块长
米的长方形空地上计划新建一块长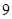 米,宽
米,宽 米的长方形花圃.
米的长方形花圃.(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多
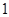 平方米,请你给出你认为合适的三种不同的方案;
平方米,请你给出你认为合适的三种不同的方案;(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加
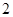
 平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.
在Rt△ABC中,∠C=90°,D,E分别为CB,CA延长线上的点,BE与AD的交点为P.

(1)若BD=AC,AE=CD,在图1中画出符合题意的图形,并直接写
 出∠APE的度数;
出∠APE的度数;(2)若
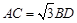 ,
,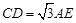 ,求∠APE的度数.
,求∠APE的度数.
如图1,平面直角坐标系 xOy中,A
xOy中,A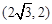 ,B
,B .将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿
.将△OAB绕点O顺时针旋转a角(0°<a<90°)得到△OCD(O,A,B的对应点分别为O,C,D),将△OAB沿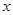 轴负方向平移m个单位得到△EFG(m>0,O,A,B的
轴负方向平移m个单位得到△EFG(m>0,O,A,B的 对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数
对应点分别为E,F,G),a,m的值恰使点C,D,F落在同一反比例函数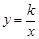 (k≠0)的图象上.
(k≠0)的图象上.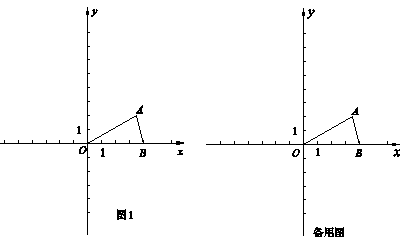
(1)∠AOB=°,a=°;
(2)求经过点A,B,F的抛物线的解析式;
(3)若(2)中抛物线的顶点为M,抛物线与直线EF的另一个交点为H,抛物线上的点P满足以P,M,F,A为顶点的四边形的面积与四边形MFAH的面积相等(点P不与点H重合),请直接写出满足条件的点P的个数,并求位于直线EF上方的点P
 的坐标.
的坐标.
抛物线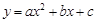 ,a>0,c<0,
,a>0,c<0,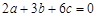 .
.(1)求证:
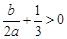 ;
;(2)抛物线经过点
 ,Q
,Q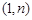 .① 判断
.① 判断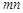 的符号;② 若抛物线与x轴的两个交点分别为点A
的符号;② 若抛物线与x轴的两个交点分别为点A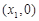 ,点B
,点B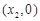 (点A在点B左)请说明
(点A在点B左)请说明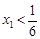 ,
,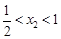 .
.