(本题满分12分)一名篮球运动员传球，球沿抛物线y＝－x2+2x+4运行，传球时，球的出手点P的高度为1.8米，一名防守队员正好处在抛物线所在的平面内，他原地竖直起跳的最大高度为3.2米，
问：（1）球在下落过
程中，防守队员原地竖直起跳后在到达最大高度时刚好将球断掉，那么传球时，两人相距多少米？（2）要使球在运行过程中不断防守队员断掉，且仍按抛物线y＝－x2+2x+4运行，那么两人间的距离应在什么范围内？（结果保留
根号）
已知2x﹣3=0，求代数式x（x2﹣x）+x2（5﹣x）﹣9的值．
解不等式组：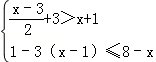
并在数轴上把解集表示出来．
已知直角坐标系中菱形ABCD的位置如图,C、D两点的坐标分别为(8,0)、(0,6).现有两动点P、Q分别从A、C同时出发,点P沿折线ADC向终点C运动, 点Q沿线段CA向终点A运动,当P、Q两点中有一点到达终点时,另一点也立即停止运动,设运动时间为t秒.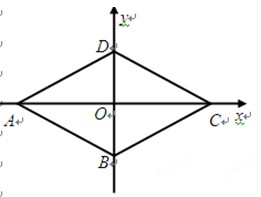
(1)填空：菱形ABCD的边长是,面积是；
(2)探究下列问题：
①若点P的速度为每秒2.5个单位,点Q的速度为每秒3个单位,求△APQ的面积S关于t的函数关系式,并求出S的最大值；
②在运动过程中,能否使得△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形,若存在,求出t的值；若不存在,请说明理由.
如图1,若△ABC和△ADE为等腰直角三角形,AB=AC,AD=AE,M,N分别EB,CD的中点．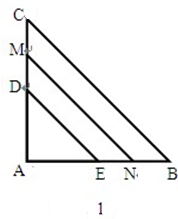
（1）易证：①CD="BE" ；②△AMN是三角形；
（2）当把△ADE绕A点旋转到图2的位置时,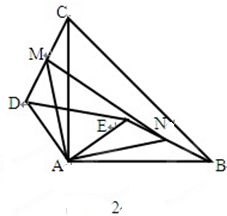
①求证：CD=BE；
②判断△AMN的形状,并证明你的结论；
（3）当△ADE绕A点旋转到图3的位置时,（2）中的结论是否成立？直接写出即可,不要求证明；并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比．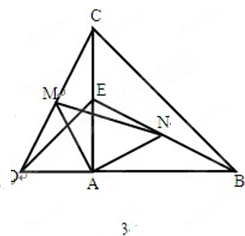
如图,在Rt△ABC中,∠C=90°,点D在AB上,以BD为直径的⊙O与AC交于点E,且BE平分∠ABC,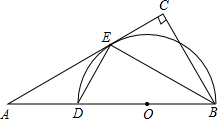
（1）判断直线AC与⊙O的位置关系,并说明理由；
（2）若AD=2,AE=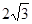
,求⊙O的面积．