如图1,若△ABC和△ADE为等腰直角三角形,AB=AC,AD=AE,M,N分别EB,CD的中点.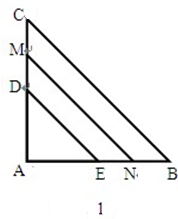
(1)易证:①CD="BE" ;②△AMN是 三角形;
(2)当把△ADE绕A点旋转到图2的位置时,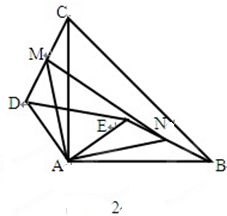
①求证:CD=BE;
②判断△AMN的形状,并证明你的结论;
(3)当△ADE绕A点旋转到图3的位置时,(2)中的结论是否成立?直接写出即可,不要求证明;并求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比.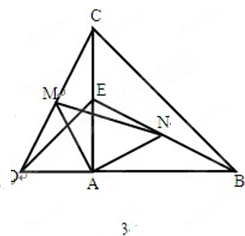
如图,点A、E、F、C在同一直线上,AD∥BC,AD=CB,AE=CE.求证:∠B=∠D.
解方程: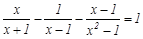 .
.
计算: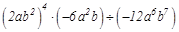 .
.
(本小题8分)如图,已知点A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.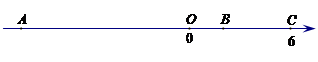
(1)数轴上点A表示的数是,点B表示的数是;
(2)动点P、Q同时从A、C出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以3个单位长度的速度沿数轴向左匀速运动,M为AP的中点, N在线段CQ上,且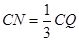 ,设运动时间为t(t>0)秒.
,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
(本小题8分)小学毕业时,六年级某班为纪念师生情谊,班委决定花800元班费买两种不同单价的留念册,分别给50位同学和10位任课老师每人一本留做纪念。其中送给任课老师的留念册的单价比给同学的单价多8元。请问这两种不同留念册的单价分别为多少元?