已知直角坐标系中菱形ABCD的位置如图,C、D两点的坐标分别为(8,0)、(0,6).现有两动点P、Q分别从A、C同时出发,点P沿折线ADC向终点C运动, 点Q沿线段CA向终点A运动,当P、Q两点中有一点到达终点时,另一点也立即停止运动,设运动时间为t秒.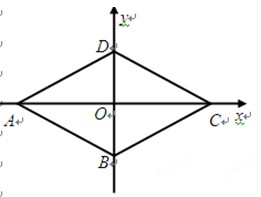
(1)填空：菱形ABCD的边长是 ,面积是 ；
(2)探究下列问题：
①若点P的速度为每秒2.5个单位,点Q的速度为每秒3个单位,求△APQ的面积S关于t的函数关系式,并求出S的最大值；
②在运动过程中,能否使得△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形,若存在,求出t的值；若不存在,请说明理由.
计算或化简：（每小题5分，共10分）
（1）
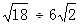（2）
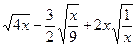
(本题12分) 如图，在平面直角坐标系xoy中，矩形ABCD的边AB在x轴上，且AB=3，BC=
，直线y=
经过点C，交y轴于点G,且∠AGO=30°。
（1）点C、D的坐标分别是C（），D（）；
（2）求顶点在直线y=上且经过点C、D的抛物线的解析式；
（3）将（2）中的抛物线沿直线y=
平移，平移后的抛物线交y轴于点F，顶点为点E。平移后是否存在这样的抛物线，使△EFG为等腰三角形？若存
在，请求出此时抛物线的解析式；若不存在，请说明理由。
某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：
，且物价部门规定这种绿茶的销售单价不得高于90元/千克．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求y与x的关系式；
（2）当x取何值时，y的值最大？
（3）如果公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？
(本题10分) 如图，直线
与反比例函数
的图象交于A
，B
两点．
（1）求
、
的值？
（2）直接写出
时x的取值范围？
（3）如图，等腰梯形OBCD中，BC//OD，OB=CD，OD边在x轴上，过点C作CE
⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，
请判断PC和PE的大小关系，并说明理由．
(本题8分)有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字
，
和－4．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为(x，y).
（1）用列表或画树状图的方法写出点Q的所有可能坐标；
（2）求点Q落在直线y=-X-2上的概率．