一个原来静止的电子,经过100 V电压加速后它的动能是多少?质量改变了百分之几?速度是多少?此时能否使用公式 ?(me=9.1×10-31 kg)
?(me=9.1×10-31 kg)
额定功率为80kW的汽车,在某平直的公路上行驶的最大速度为20m/s,汽车的质量
m= 2×103kg,如果汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动过程中阻力不变。
(g="10" m/s2)求:
(1)汽车所受的恒定阻力是多大?
(2)匀加速直线运动的时间是多少?
(3)匀加速运动过程中,牵引力做的功是多少?
我国在2011年10月24日发射第二颗月球卫星——“嫦娥二号”.同学们也对月球有了更多的关注.
⑴若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径r;
⑵若宇航员随登月飞船登陆月球后,在月球表面某处以速度v0 竖直向上抛出一个小球,经过时间t,小球落回抛出点.已知月球半径为R月,万有引力常量为G ,试求出月球的质量M月.
如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿y轴负方向的匀强电场;第四象限无电场和磁场。现有一质量为m、电荷量为q的粒子以速度v0从y轴上的M点沿x轴负方向进入电场,不计粒子的重力,粒子经x轴上的N点和P点最后又回到M点,设OM=L,ON=2L。求: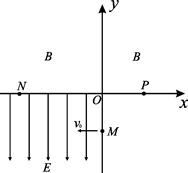
(1)电场强度E的大小;
(2)匀强磁场的磁感应强度的大小和方向;
(3)粒子从M点进入电场经N、P点最后又回到M点所用的时间。
(18分)如图,粗糙斜面与光滑水平面通过光滑小圆弧平滑连接,斜面倾角θ=37°。A、B是两个质量均为m="l" kg的小滑块(可看作质点),B的左端连接一轻质弹簧。若滑块A在斜面上受 到F="4" N,方向垂直斜面向下的恒力作用时,恰能沿斜面匀速下滑。现撤去F,让滑块A从斜面上距斜面底端L=1m处由静止开始下滑。(取g="10" m/s2,sin37°=0.6,cos37°=0.8。)
(1)求滑块A与斜面间的动摩擦因数;
(2)求滑块A到达斜面底端时的速度大小;
(3)滑块A与弹簧接触后粘连在一起,求此后弹簧的最大弹性势能。
质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s。耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,所受阻力恒定。连接杆的质量不计且与水平面的夹角θ保持不变(可认为杆中的弹力是沿着杆的方向的)。求:
(1)拖拉机的加速度大小。
(2)拖拉机对连接杆的拉力大小。