(本题满分15分 )已知函数 .
.
(1)求函数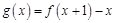 的最大值;
的最大值;
(2)若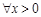 ,不等式
,不等式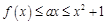 恒成立,求实数
恒成立,求实数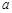 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: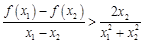 .
.
.设集合 ,
,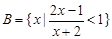 ,全集为R
,全集为R
(1)当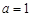 时,求:
时,求: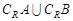 ;
;
(2)若 ,求实数
,求实数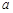 的取值范围.
的取值范围.
(3)当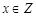 时,求B的非空真子集的个数;
时,求B的非空真子集的个数;
(本小题满分12分)
已知二次函数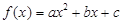 .
.
(1)若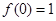 ,
,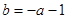 ,解关于x不等式
,解关于x不等式 ;
;
(2)若f(x)的最小值为0,且A.<b,设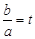 ,请把
,请把 表示成关于t的函数g(t),并求g(t)的最小值.
表示成关于t的函数g(t),并求g(t)的最小值.
(本小题满分12分)
如图1,在三棱锥P-A.BC中,PA.⊥平面A.BC,A.C⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示.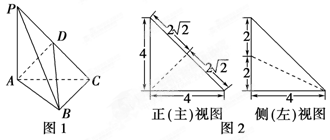
(1) 证明:A.D⊥平面PBC;
(2) 求三棱锥D-A.BC的体积;
(3) 在∠A.CB的平分线上确定一点Q,使得PQ∥平面A.BD,并求此时PQ的长.
(本小题满分12分)
在数列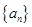 中,
中,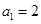 ,
,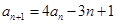 ,
, .
.
(1)证明数列 是等比数列;
是等比数列;
(2)求数列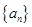 的前
的前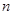 项和
项和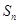 ;
;
(3)证明不等式 ,对任意
,对任意 皆成立.
皆成立.
(本小题满分12分)
设实数x,y满足不等式组: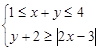
(1)求作点(x,y)所在的平面区域;
(2)设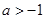 ,在(1)所求的区域内,求函数
,在(1)所求的区域内,求函数 的最大值和最小值。
的最大值和最小值。