商店出售茶壶和茶杯,茶壶定价每个20元,茶杯每个5元,该商店推出两种优惠办法:(1)买一个茶壶赠一个茶杯;(2)按总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),若购买茶杯数x个,付款y(元),分别建立两种优惠办法中y与x之间的函数关系式,并讨论该顾客买同样多的茶杯时,两种办法哪一种更优惠。
(本小题满分13分)设函数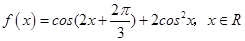 .
.
(Ⅰ)求函数f(x)的最小正周期和单调减区间;
(Ⅱ)将函数f(x)的图象向右平移 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间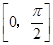 上的最小值.
上的最小值.
(本小题满分14分)已知函数 (aÎR).
(aÎR).
(Ⅰ)当a=2时,求函数 在(1, f(1))处的切线方程;
在(1, f(1))处的切线方程;
(Ⅱ)当a>0时,求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 有两个极值点
有两个极值点 ,
,  (
( ),不等式
),不等式 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分13分)已知动点P到定点 的距离和它到定直线
的距离和它到定直线 的距离的比值为
的距离的比值为 .
.
(Ⅰ)求动点P的轨迹W的方程;
(Ⅱ)若过点F的直线与点P的轨迹W相交于M,N两点(M,N均在y轴右侧),点 、
、 ,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
,设A,B,M,N四点构成的四边形的面积为S,求S的取值范围.
(本小题满分12分)如图,三棱柱ABC-A1B1C1中,平面ABB1A1⊥底面ABC, ,∠A1AB=120°,D、E分别是BC、A1C1的中点.
,∠A1AB=120°,D、E分别是BC、A1C1的中点.
(Ⅰ)试在棱AB上找一点F,使DE∥平面A1CF;
(Ⅱ)在(Ⅰ)的条件下,求多面体BCF-A1B1C1的体积.
(本小题满分12分)已知数列{an},{bn}满足:a1b1+a2b2+a3b3+…+anbn= (
( ).
).
(Ⅰ)若{bn }是首项为1,公比为2等比数列,求数列{an}的通项公式;
(Ⅱ)在数列{an}中,a1=1,对任意 ,
, ,记数列{an+bn}的前n项和为Tn,求满足不等式
,记数列{an+bn}的前n项和为Tn,求满足不等式 的自然数n的最小值.
的自然数n的最小值.