如图,△ABC中,AB=AC,E,D分别是AB,AC上的点,连接BD,CE.请你增加一个条件(不再添加其它线段,不再标注其它字母),使BD=CE,并加以证明.
你添加的条件是:________________________________.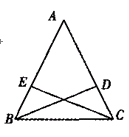
已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离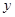 与行驶时间
与行驶时间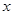 之间的函数图象.
之间的函数图象.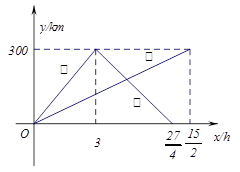
(1)请直接写出甲、乙两车离各自出发地的距离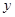 与行驶时间
与行驶时间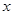 之间的函数关系式,并标明自变量
之间的函数关系式,并标明自变量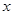 的取值范围;
的取值范围;
(2)它们在行驶过程中有几次相遇?并求出每次相遇的时间.
如图,沿AC方向开山修一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=127º,沿BD的方向前进,取∠BDE=37º,测得BD=520m,并且AC、BD和DE在同一平面内.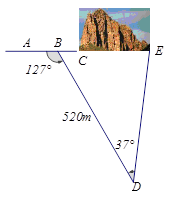
(1)施工点E 离D多远正好能使A、C、E成一直线(结果保留整数)
(2)在(1)的条件下,若BC=80m,求公路CE段的长(结果保留整数)
(参考数据:sin37º≈0.60, cos37º≈ 0.80, tan37º≈0.75))
如图,抛物线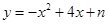 经过点A(1,0),与
经过点A(1,0),与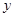 轴交于点B.
轴交于点B.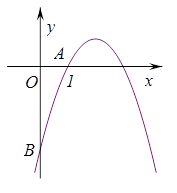
(1)求抛物线的解析式和顶点坐标;
(2)若P是坐标轴上一点,且三角形PAB是以AB为腰的等腰三角形,试求P点坐标.
如图,AB是O的直径,C为AB延长线上一点,CD交O于点D,且∠A=∠C=30º.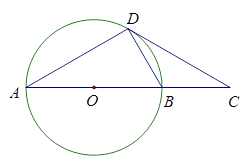
(1)证明CD是的切线;
(2)请你写出线段BC和AC之间的数量关系,并证明.
某校德育处为了解学生对城市核心价值观中哪一项内容最感兴趣,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图,请你结合图中信息解答下列问题:

图1图2
(1)填空:该校共调查了名学生;
(2)请分别把条形统计图和扇形统计图补充完整;
(3)若该校共有3 000名学生,请你估计全校对“诚信”最感兴趣的人数.