如图,抛物线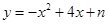 经过点A(1,0),与
经过点A(1,0),与 轴交于点B.
轴交于点B.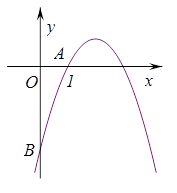
(1)求抛物线的解析式和顶点坐标;
(2)若P是坐标轴上一点,且三角形PAB是以AB为腰的等腰三角形,试求P点坐标.
已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.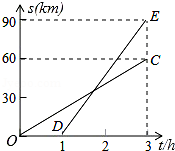
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.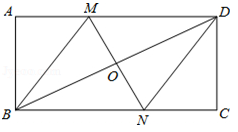
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
某公司招聘人才,对应聘者分别进行阅读能力,思维能力和表达能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)
| 项目 人员 |
阅读 |
思维 |
表达 |
| 甲 |
93 |
86 |
73 |
| 乙 |
95 |
81 |
79 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
如图,已知四边形ABCD是平行四边形.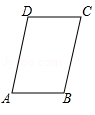
(1)作∠A的平分线交BC于点E.(用尺规作图,保留作图痕迹,不用写作法)
(2)在(1)中,若AD=6,EC=2,求平行四边形ABCD的周长.
已知一次函数的图象经过点A(1,1)和点B(2,﹣1),求这个一次函数的解析式.