计算: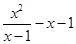 ;
;
(本小题满分8分)新华商场销售某种空调,每台进货价为2500元。市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台。商场要想使这种空调的销售利润平均每天达到5000元,每台空调的定价应为多少元?
(本小题满分10分)如图,为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据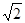 ≈1.41,
≈1.41,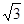 ≈1.73)
≈1.73)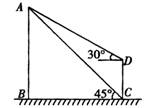
红光服装厂要生产某种学生服一批,已知每3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产学生服,应分别用多少布料生产上衣和裤子,才能恰好配套?共能生产多少套?
一家商店将某种服装按进价提高40%后标价,又以8折优惠卖出,结果每件仍获利15元,这种服装每件的进价是多少?
如图三角形ABC中,∠ACB=90°,CD是AB边上的高。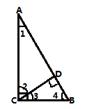
(1)写出图中三对互余的角;
(2)你认为∠1与∠3相等吗?说明你你的理由。