(本小题满分13分)为增强市民交通规范意识,我市面向全市征召劝导员志愿者,分布于各候车亭或十字路口处.现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示.
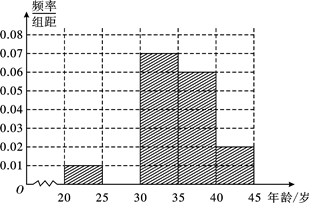
(1)频率分布表中的①、②位置应填什么数据?并在答题卡中补全频率分布直方图(如图),再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数;
(2)在抽出的100名志愿者中按年龄再采用分层抽样法抽取20人参加“规范摩的司机的交通意识”培训活动,从这20人中选取2名志愿者担任主要负责人,记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
| 分组(单位:岁) |
频数 |
频率 |
| [20,25) |
5 |
0.05 |
| [25,30) |
① |
0.20 |
| [30,35) |
35 |
② |
| [35,40) |
30 |
0.30 |
| [40,45] |
10 |
0.10 |
| 合计 |
100 |
1.00 |
若三点A(2,-3)、B(4,3)、C(5,k)在同一条直线上,请求出k的取值.
圆 内有一点
内有一点 ,AB为过点
,AB为过点 且倾斜角为α的弦,
且倾斜角为α的弦,
(1)当 时,求AB的长;
时,求AB的长;
(2)当弦AB被点 平分时,写出直线AB 的方程。
平分时,写出直线AB 的方程。
甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,速度不得超过50千米/ 小时。已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v千米/小时的平方成正比,比例系数为0.02;固定部分为50元/小时.
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
 的三个顶点是
的三个顶点是 ,
, ,
, .
.
(1)求BC边的高所在直线方程;(2)求 的面积S.
的面积S.
函数 的定义域集合是A,函数
的定义域集合是A,函数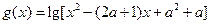 的定义域集合是B
的定义域集合是B
(1)求集合A、B;
(2)若A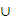 B=B,求实数
B=B,求实数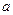 的取值范围.
的取值范围.