甲、乙两地相距200千米,汽车从甲地匀速行驶到乙地,速度不得超过50千米/ 小时。已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v千米/小时的平方成正比,比例系数为 0.02;固定部分为50元/小时.
(1)把全程运输成本y(元)表示为速度v(千米/时)的函数,并指出定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
(本小题满分12分) 甲乙共同拥有一块形状为等腰三角形的地ABC,其中 。如果画一条线使两块地面积相等,其中两端点P、Q分别在线段AB,AC上。
。如果画一条线使两块地面积相等,其中两端点P、Q分别在线段AB,AC上。
(1)如果建一条篱笆墙,如何划线建墙费用最低?
(2)如果在PQ线上种树,如何划线种树最多?
(本小题满分12分)已知数列 的前n项和
的前n项和 ,且
,且 是
是 与1的等差中项。
与1的等差中项。
(1)求数列 和数列
和数列 的通项公式;
的通项公式;
(2)若 ,求
,求
(3)若 ,是否存在
,是否存在 ,使得
,使得 并说明理由。
并说明理由。
(本小题满分12分)已知函数 (其中e为自然对数)
(其中e为自然对数)
(1)求F(x)="h" (x) 的极值。
的极值。
(2)设 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(本小题满分12分)如图,多面体 的直观图及三视图如图所示,
的直观图及三视图如图所示,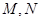 分别为
分别为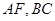 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)求多面体 的体积。
的体积。
(本小题满分10分)已知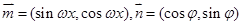 ,函数
,函数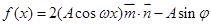 (其中
(其中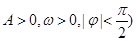 的图像在
的图像在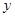 轴右侧的第一个最高点(即函数取得最大值的点)为
轴右侧的第一个最高点(即函数取得最大值的点)为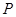
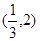 ,在原点右侧与
,在原点右侧与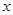 轴的第一个交点为
轴的第一个交点为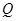
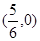 .
.
(1)求函数 的表达式;
的表达式;
(2)判断函数 在区间
在区间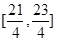 上是否存在对称轴,存在求出方程;否则说明理由;
上是否存在对称轴,存在求出方程;否则说明理由;