如图，平面PCBM⊥平面ABC,∠PCB=90°,PM∥BC,直线AM与直线PC所成的角为60°，又AC=1,BC=2PM=2,∠ACB="90° "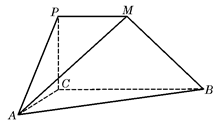 
(1)求证：AC⊥BM;
(2)求二面角M-AB-C的余弦值
（3求P到平面MAB的距离
10分）已知圆C的圆心在直线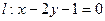
上，并且经过A（2，1）B（1，2）两点，求圆C的标准方程．
已知以函数
的图象上的点
为切点的切线的倾斜角为
．
（1）求
的值；
（2）是否存在正整数
，使不等式
对于
恒成立？若存在，求出最小的正整数，若不存在，说明理由；
（3）对于
，比较
与
的大小．
函数
对任意实数
都有
.
（1）若
，求
的值；
（2）对于任意
，求证：
；
（3）若
，求证：
.
抛一枚均匀的骰子（骰子的六面分别有数字1、2、3、4、5、6）来构造数列
，且
，记
.
（1）求
的概率；
（2）求
，
的概率；
(3)若记
,求
.
某突发事件，在不采取任何预防措施的情况下发生的概率为
，一旦发生，将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择，单独采用甲、乙预防措施所需的费用分别为40万元和20万元，采用相应预防措施后此突发事件不发生的概率分别为
和
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用，请分别计算这几种预防方案的总费用，并指出哪一种预防方案总费用最少.
(注：总费用 = 采取预防措施的费用+发生突发事件损失的期望值)