某突发事件,在不采取任何预防措施的情况下发生的概率为 ,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为
,一旦发生,将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择,单独采用甲、乙预防措施所需的费用分别为40万元和20万元,采用相应预防措施后此突发事件不发生的概率分别为 和
和 .若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用,请分别计算这几种预防方案的总费用,并指出哪一种预防方案总费用最少.
(注:总费用 = 采取预防措施的费用+发生突发事件损失的期望值)
给定椭圆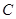 :
:
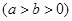 ,称圆心在原点
,称圆心在原点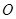 ,半径为
,半径为 的圆是椭圆
的圆是椭圆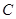 的“准圆”.若椭圆
的“准圆”.若椭圆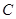 的一个焦点为
的一个焦点为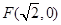 ,且其短轴上的一个端点到
,且其短轴上的一个端点到 的距离为
的距离为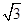 .
.
(Ⅰ)求椭圆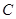 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(Ⅱ)点 是椭圆
是椭圆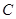 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线 ,使得
,使得 与椭圆
与椭圆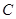 都只有一个交点,试判断
都只有一个交点,试判断 是否垂直,并说明理由.
是否垂直,并说明理由.
如图,四棱锥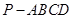 中,
中,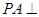 底面
底面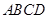 ,四边形
,四边形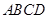 中,
中, ,
,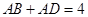 ,
,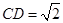 ,
, .
.
(Ⅰ)求证:平面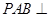 平面
平面 ;
;
(Ⅱ)设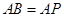 .
.
(ⅰ) 若直线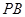 与平面
与平面 所成的角为
所成的角为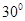 ,求线段
,求线段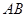 的长;
的长;
(ⅱ) 在线段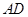 上是否存在一个点
上是否存在一个点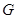 ,使得点
,使得点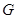 到点
到点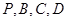 的距离都相等?说明理由.
的距离都相等?说明理由.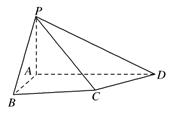
(本小题满分12分)等差数列 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为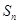 ,等比数列
,等比数列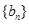 中,
中,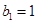 ,
,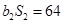 ,
,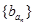 是公比为64的等比数列.
是公比为64的等比数列.
(Ⅰ)求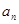 与
与 ;
;
(Ⅱ)证明: .
.
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量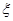 表示密码中不同数字的个数.
表示密码中不同数字的个数.
(Ⅰ)求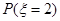 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量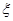 的分布列和它的数学期望.
的分布列和它的数学期望.
已知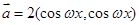 ,
, (其中
(其中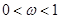 ),函数
),函数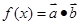 ,若直线
,若直线 是函数
是函数 图象的一条对称轴.
图象的一条对称轴.
(Ⅰ)试求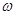 的值;
的值;
(Ⅱ)若函数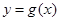 的图象是由
的图象是由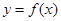 的图象的各点的横坐标伸长到原来的2倍,然后再向左平移
的图象的各点的横坐标伸长到原来的2倍,然后再向左平移 个单位长度得到,求
个单位长度得到,求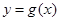 的单调递增区间.
的单调递增区间.