如图,四棱锥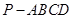 中,
中,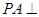 底面
底面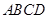 ,四边形
,四边形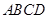 中,
中, ,
,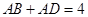 ,
,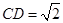 ,
, .
.
(Ⅰ)求证:平面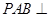 平面
平面 ;
;
(Ⅱ)设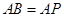 .
.
(ⅰ) 若直线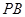 与平面
与平面 所成的角为
所成的角为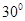 ,求线段
,求线段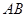 的长;
的长;
(ⅱ) 在线段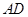 上是否存在一个点
上是否存在一个点 ,使得点
,使得点 到点
到点 的距离都相等?说明理由.
的距离都相等?说明理由.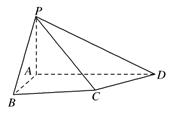
(本题满分12分)已知三个集合
A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-bx+2=0},问同时满足B  A、C
A、C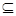 A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
设集合P={4,3t+2,5t2},Q={3t-2,5t-6,5t2-1},且P∩Q={4},求实数t及P∪Q.
已知A={1,x,y},B={x,x2,xy}且A=B,求x、y;
(本小题满分10分)已知集合A={x|x2-3x+2=0},B={x|x2-ax+3a-5=0}.若A∩B=B,求实数a的取值范围.
(本小题满分10分) 已知A={x|x2-ax+a2-19=0},B={x|x2-5x+8=2},C={x|x2+2x-8=0}.若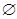
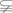 A∩B,且A∩C=
A∩B,且A∩C=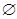 ,求a的值.
,求a的值.