(本题满分12分)已知三个集合
A={x|x2-3x+2=0},B={x|x2-ax+(a-1)=0},C={x|x2-bx+2=0},问同时满足B  A、C
A、C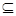 A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
A的实数a、b是否存在?若存在,求出a、b所有值的集合;若不存在,请说明理由.
为了降低能损耗,最近上海对新建住宅的屋顶和外墙都要求建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能消耗费用为8万元.设f(x)为隔热层建造费用与20年的能消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.
已知点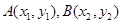 是函数
是函数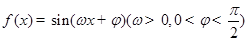 图象上的任意两点,若
图象上的任意两点,若 时,
时,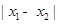 的最小值为
的最小值为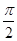 ,且函数
,且函数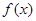 的图像经过点
的图像经过点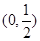 .
.
(Ⅰ)求函数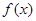 的解析式;
的解析式;
(Ⅱ)在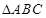 中,角
中,角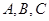 的对边分别为
的对边分别为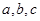 ,且
,且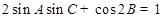 ,求
,求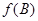 的取值范围.
的取值范围.
设 和
和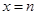 是函数
是函数 的两个极值点,其中
的两个极值点,其中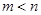 ,
, .
.
(1)求 的取值范围;
的取值范围;
(2)若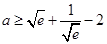 ,求
,求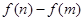 的最大值.注:e是自然对数的底.
的最大值.注:e是自然对数的底.
如图,在梯形 中,
中,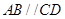 ,
, ,
, ,平面
,平面 平面
平面 ,四边形
,四边形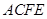 是矩形,
是矩形,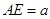 ,点
,点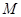 在线段EF上.
在线段EF上.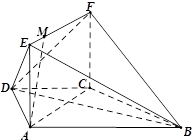
(1)求异面直线 与
与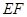 所成的角;
所成的角;
(2)求二面角 的余弦值.
的余弦值.
已知数列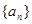 ,
, ,
, ,
,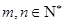 .
.
(1)求证: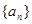 为等比数列,并求出通项公式
为等比数列,并求出通项公式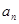 ;
;
(2)记数列  的前
的前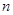 项和为
项和为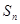 且
且 ,求
,求
 .
.