已知数列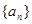 ,
, ,
, ,
,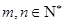 .
.
(1)求证: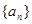 为等比数列,并求出通项公式
为等比数列,并求出通项公式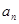 ;
;
(2)记数列  的前
的前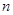 项和为
项和为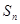 且
且 ,求
,求
 .
.
设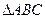 的内角
的内角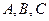 所对的边分别为
所对的边分别为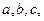 且
且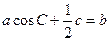 .(1)求角
.(1)求角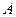 的大小;(2)若
的大小;(2)若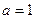 ,求
,求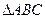 的周长
的周长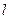 的取值范围.
的取值范围.
如图,抛物线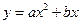 (a
(a 0)与双曲线
0)与双曲线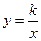 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.
某商店以6元/千克的价格购进某种干果1140千克,并对其进行筛选分成甲级干果与乙级干果后同时开始销售。这批干果销售结束后,店主从销售统计中发出:甲级干果与乙级干果在销售过程中每天都有销量,且在同一天卖完;甲级干果从开始销售至销售的第 天的总销量
天的总销量 (千克)与
(千克)与 的关系为
的关系为 ;乙级干果从开始销售至销售的第
;乙级干果从开始销售至销售的第 天的总销量
天的总销量 (千克)与
(千克)与 的关系为
的关系为 ,且乙级干果的前三天的销售量的情况见下表:
,且乙级干果的前三天的销售量的情况见下表:
(1)求 、
、 的值;
的值;
(2)若甲级干果与乙级干果分别以8元/千克的6元/千克的零售价出售,则卖完这批干果获得的毛利润是多少元?
(3)问从第几天起乙级干果每天的销量比甲级干果每天的销量至少多6千克?
(说明:毛利润=销售总金额-进货总金额。这批干果进货至卖完的过程中的损耗忽略不计)
如图,⊙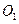 与⊙
与⊙ 相交于点A和B,经过A作直线与⊙
相交于点A和B,经过A作直线与⊙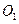 相交于D,与⊙
相交于D,与⊙ 相交于C,设弧
相交于C,设弧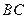 的中点为M,弧
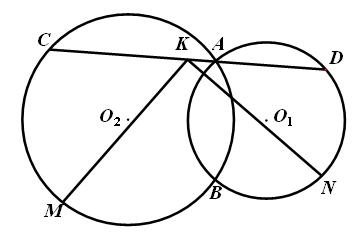
的中点为M,弧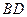 的中点为N,线段CD的中点为K. 求证:
的中点为N,线段CD的中点为K. 求证: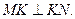
(1)已知 ,求
,求 的值。
的值。
(2)已知 是方程
是方程 的一个根,试求
的一个根,试求 的值。
的值。