已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为 的正方形(记为
的正方形(记为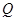 )
)
(Ⅰ)求椭圆 的方程
的方程
(Ⅱ)设点 是直线
是直线 与
与 轴的交点,过点
轴的交点,过点 的直线
的直线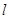 与椭圆
与椭圆 相交于
相交于 两点,当线段
两点,当线段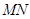 的中点落在正方形
的中点落在正方形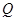 内(包括边界)时,求直线
内(包括边界)时,求直线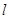 斜率的取值范围
斜率的取值范围
为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 对别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
(Ⅰ)从这18名队员中随机选出两名,求两人来自同一队的概率;
(Ⅱ)中国女排奋力拼搏,战胜了韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望
如图,四棱锥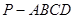 中,底面
中,底面 为梯形,
为梯形,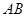 ∥
∥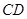 ,
, 
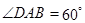 ,
, 平面
平面 ,
,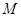 为
为 的中点
的中点
(Ⅰ)证明:
(Ⅱ)若 ,求二面角
,求二面角 的余弦值
的余弦值
在△ABC中,角 所对的边分别为
所对的边分别为 ,
, 且
且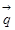 ∥
∥
(Ⅰ)求 的值
的值
(Ⅱ)求三角函数式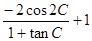 的取值范围
的取值范围
已知数列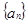 的前
的前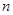 项和
项和 满足
满足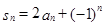 ,
,
(Ⅰ)求数列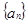 的前三项
的前三项
(Ⅱ)设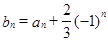 ,求证:数列
,求证:数列 为等比数列,并指出
为等比数列,并指出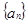 的通项公式。
的通项公式。