已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为
轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为 的正方形(记为
的正方形(记为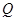 )
)
(Ⅰ)求椭圆 的方程
的方程
(Ⅱ)设点 是直线
是直线 与
与 轴的交点,过点
轴的交点,过点 的直线
的直线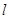 与椭圆
与椭圆 相交于
相交于 两点,当线段
两点,当线段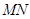 的中点落在正方形
的中点落在正方形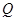 内(包括边界)时,求直线
内(包括边界)时,求直线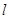 斜率的取值范围
斜率的取值范围
(本小题满分13分)
设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4(a0,a1,a2,a3,a4∈R)当x=-1时,f(x)取得极大值,且函数y=f(x+1)的图象关于点(-1,0)对称.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-,]上;
(Ⅲ)设xn=,ym=(m,n∈N),求证:|f(xn)-f(ym)|<.
(本小题满分13分)
如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.
.(本小题满分13分)
将3封不同的信投进A、B、C、D这4个不同的信箱、假设每封信投入每个信箱的可能性相等.
(Ⅰ)求这3封信分别被投进3个信箱的概率;
(Ⅱ)求恰有2个信箱没有信的概率;
(Ⅲ)求A信箱中的信封数量的分布列和数学期望.
.(本小题满分13分)
已知函数f(x)=sinωx·cosωx-cos2ωx(ω>0)的最小正周期为.
(Ⅰ)求ω的值;
(Ⅱ)设△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,求此时f(x)的值域.
(本小题满分14分)
已 知直线
知直线 :
: 与圆
与圆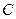 :
: 相交于
相交于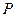 、
、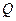 两点,点
两点,点 满足
满足 .
.
(Ⅰ)当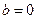 时,求实数
时,求实数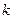 的值;
的值;
(Ⅱ)当 时,求实数
时,求实数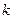 的取值范围;
的取值范围;
(Ⅲ)设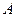 、
、 是圆
是圆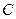 :
: 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆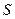 ,使直线
,使直线 恒与圆
恒与圆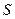 相切.
相切.