为了降低能损耗，最近上海对新建住宅的屋顶和外墙都要求建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能消耗费用C(单位：万元)与隔热层厚度x(单位：cm)满足关系：C(x)＝(0≤x≤10)，若不建隔热层，每年能消耗费用为8万元．设f(x)为隔热层建造费用与20年的能消耗费用之和．
(1)求k的值及f(x)的表达式；
(2)隔热层修建多厚时，总费用f(x)达到最小，并求最小值．
（本小题满分10分）已知函数f（x）＝
的定义域为集合A，函数g（x）＝lg（－x2＋2x＋m）的定义域为集合B.
（1）当m＝3时，求A∩（∁RB）；
（2）若A∩B＝{x|－1＜x＜4}，求实数m的值．
（本小题满分14分）已知函数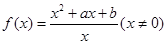
是奇函数，且满足
（1）求实数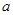
、
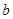的值；
（2）试证明函数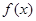
在区间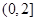
单调递减，在区间
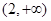单调递增；
（3）是否存在实数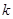
同时满足以下两个条件：
①不等式
对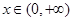
恒成立；②方程
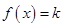在
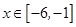上有解．
若存在，试求出实数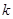的取值范围，若不存在，请说明理由．
（本小题满分14分）某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
| 组号 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
| 分组 |
[50，60） |
[60，70） |
[70，80） |
[80，90） |
[90，100] |
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均分；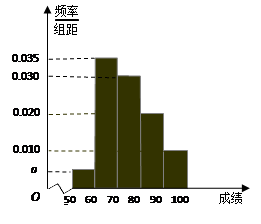
（3）现用分层抽样的方法从第3、4、5组中随机抽取6名学生，将该样本看成一个总体，从中随机抽取2名，求其中恰有1人的分数不低于90分的概率？
（本小题满分13分）设关于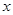
的一元二次方程
.
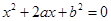（1）若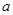
是从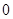
、
、
、
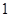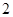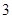四个数中任取的一个数，
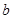是从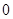、、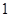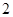三个数中任取的一个数，求上述方程有实根的概率；
（2）若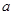
是从区间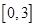
任取的一个数，
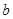是从区间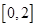
任取的一个数，求上述方程有实根的概率.
（本小题满分13分）如图，∠AOB＝60°，OA＝2，OB＝5，在线段OB上任取一点C，试求：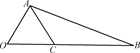
（1）△AOC为钝角三角形的概率；
（2）△AOC为锐角三角形的概率．