（本小题满分14分）已知函数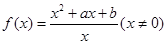
是奇函数，且满足
（1）求实数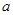
、
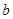的值；
（2）试证明函数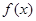
在区间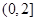
单调递减，在区间
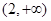单调递增；
（3）是否存在实数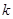
同时满足以下两个条件：
①不等式
对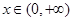
恒成立；②方程
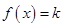在
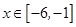上有解．
若存在，试求出实数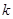的取值范围，若不存在，请说明理由．
已知a，b为正实数．
(1)求证：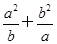
≥a＋b；
(2)利用(1)的结论求函数y＝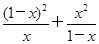
(0<x<1)的最小值．
已知函数f(x)＝|x＋3|＋|x－a|(a>0)．
(1)当a＝4时，已知f(x)＝7，求x的取值范围；
(2)若f(x)≥6的解集为{x|x≤－4或x≥2}，求a的值．
设函数f(x)＝|x－1|＋|x－2|.
(1)画出函数y＝f(x)的图象；
(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．
设不等式|x－2|<a(a∈N*)的解集为A，且
∈A，
∉A.
(1)求a的值；
(2)求函数f(x)＝|x＋a|＋|x－2|的最小值．
已知a≥b>0，求证：2a3－b3≥2ab2－a2b.