(本小题满分12分)
计算机考试分理论考试与上机操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中合格的概率分别为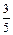 ,
,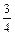 ,
,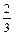 ;在上机操作考试中合格的概率分别为
;在上机操作考试中合格的概率分别为 ,
,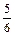 ,
,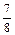 .所有考试是否合格相互之间没有影响.
.所有考试是否合格相互之间没有影响.
(Ⅰ)甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大?
(Ⅱ)求这三人计算机考试都获得“合格证书”的概率;
(Ⅲ)用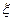 表示甲、乙、丙三人在理论考核中合格人数,求
表示甲、乙、丙三人在理论考核中合格人数,求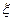 的分布列和数学期望
的分布列和数学期望 .
.
(本小题满分14分)
已知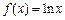 ,
,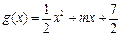 (
(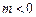 ),直线
),直线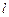 与函数
与函数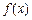 、
、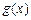 的图像都相切,且与函数
的图像都相切,且与函数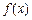 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(1)求直线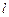 的方程及
的方程及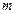 的值;
的值;
(2)若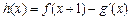 (其中
(其中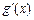 是
是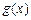 的导函数),求函数
的导函数),求函数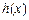 的最大值;
的最大值;
(3)当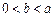 时,比较
时,比较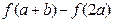 与
与 .
.
(本小题满分14分)
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,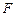 为
为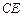 上的点,且BF
上的点,且BF
⊥平面ACE. (1)求证:AE⊥BE;
(1)求证:AE⊥BE;
(2)求三棱锥D-AEC的体积;
(3)设M在线段AB上,且满足AM=2MB,试
在线段CE上确定一点N,使得MN∥平面DAE.
(本小题满分12分)
已知集合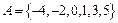 ,在平面直角坐标系中,点
,在平面直角坐标系中,点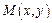 的坐标x∈A,y∈A.计算:
的坐标x∈A,y∈A.计算:
(1)点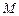 正好在第二象限的概率;
正好在第二象限的概率;
(2)点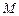 不在x轴上的概率;
不在x轴上的概率;
(3)点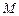 正好落在区域
正好落在区域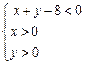 上的概率.
上的概率.
(本小题满分12分)
已知x是三角形的内角,且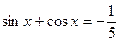 .
.
(Ⅰ)求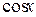 的值;
的值;
(Ⅱ)求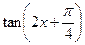 的值.
的值.
(本小题14分)设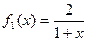 ,定义
,定义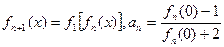 ,其中
,其中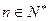 .
.
(1)求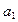 的值;
的值;
(2)求数列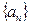 的通项公式;
的通项公式;
(3)若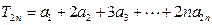 ,求
,求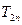 的值.
的值.