(本小题满分12分)
如右图,四边形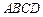 是圆柱
是圆柱 的轴截面,点
的轴截面,点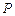 在圆柱
在圆柱 的底面圆周上,
的底面圆周上, 是
是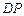 的中点,圆柱
的中点,圆柱 的底面圆的半径
的底面圆的半径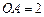 ,侧面积为
,侧面积为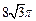 ,
,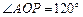 .
.
(Ⅰ)求证: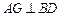 ;
;
(Ⅱ)求二面角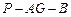 的平面角的余弦值.
的平面角的余弦值.
如图,在三棱锥 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面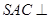 平面
平面 ,
,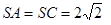 ,
,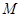 为
为 的中点.
的中点.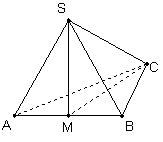
(1)证明: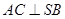 ;
;
(2)求二面角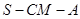 的余弦值;
的余弦值;
(3)求点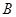 到平面
到平面 的距离.
的距离.
设函数

求证:当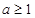 时,函数
时,函数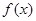 在区间
在区间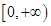 上是单调递减函数;
上是单调递减函数;
求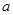 的取值范围,使函数
的取值范围,使函数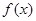 在区间
在区间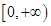 上是单调函数.
上是单调函数.
已知一个圆锥的母线长为20cm,当圆锥的高为多少时体积最大?最大体积是多少?
(1)已知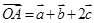 ,
,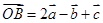 ,
,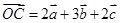 ,
,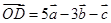 ,其中
,其中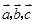 三向量不共面.试判断A,B,C,D四点是否共面?
三向量不共面.试判断A,B,C,D四点是否共面?
(2)设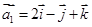 ,
,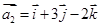 ,
,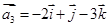 ,
,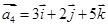 .试问是否存在实数
.试问是否存在实数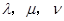 ,使
,使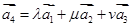 成立?如果存在,求出
成立?如果存在,求出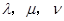 ;如果不存在,请给出理由.
;如果不存在,请给出理由.
企业管理者通过对某电子产品制造厂做上午班工人工作效率的研究表明,一个中等技术水平的工人,从8:00开始工作,t小时后可装配某电子产品的个数为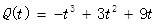 ,则这个工人从8:00到12:00何时的工作效率最高?
,则这个工人从8:00到12:00何时的工作效率最高?