如图,在三棱锥 中,
中, 是边长为4的正三角形,平面
是边长为4的正三角形,平面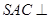 平面
平面 ,
,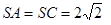 ,
,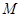 为
为 的中点.
的中点.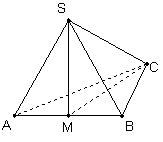
(1)证明: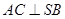 ;
;
(2)求二面角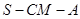 的余弦值;
的余弦值;
(3)求点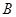 到平面
到平面 的距离.
的距离.
.(本小题满分13分)
银河科技有限公司遇到一个技术难题,隧紧急成立甲、乙两个攻关小组,按要求各自独立进行为期一月的技术攻关,同时决定在攻关期满对攻克难题的小组 给予奖励,已知这
给予奖励,已知这 些技术难题在攻关期满时被甲小组攻克的概率为
些技术难题在攻关期满时被甲小组攻克的概率为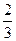 ,被乙小组攻克的概率为
,被乙小组攻克的概率为 。
。
(I)设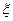 为攻关期满时获奖小组的个数,求
为攻关期满时获奖小组的个数,求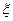 的分布列;
的分布列; (Ⅱ)设
(Ⅱ)设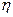 为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖小组数与没有获奖的攻关小组数之差的平方,记“函数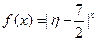 在定义域
在定义域 内单调递减“为事件
内单调递减“为事件 ,求事件
,求事件 发生的概率。
发生的概率。
(本小题满分13分)
在一个盒子中,放有标号分别为2,3,4的三张卡片,现从 这个盒子中,有放回地先后抽得两张卡片的标号分别为x,y,记
这个盒子中,有放回地先后抽得两张卡片的标号分别为x,y,记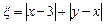 .
.
(I)求随机变量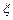 的最大值,并求事件“
的最大值,并求事件“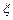 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量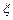 的分布列和数学期望.
的分布列和数学期望.
已知命题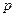
 :
:
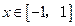 ,不等式
,不等式 恒成立;命题
恒成立;命题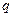 :只有一个实数
:只有一个实数 满足不等式
满足不等式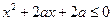 ,若命题“p或q”是真命题,“非q”是真命题,求实数a的取值范围.
,若命题“p或q”是真命题,“非q”是真命题,求实数a的取值范围.
((本小题满分14分)
已知函数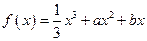 的极大值点为
的极大值点为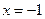 .
.
(1)用实数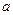 来表示实数
来表示实数 ,并求
,并求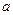 的取值范围;
的取值范围;
(2)当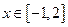 时,
时, 的最小值为
的最小值为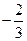 ,求
,求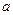 的值;
的值;
(3)设 ,
,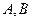 两点的连线斜率为
两点的连线斜率为 .
.
求证:必存在 ,使
,使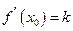 .
.
(本小题满分12分)
已知椭圆C的左、右焦点坐标分别是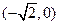 ,
,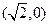 ,离心率是
,离心率是 ,直线
,直线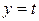 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
(1)求椭圆C的方程;
(2)若圆P经过原点,求 的值;
的值;
(3)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值。