函数 对任意实数
对任意实数 都有
都有 .
.
(1)若 ,求
,求 的值;
的值;
(2)对于任意 ,求证:
,求证: ;
;
(3)若 ,求证:
,求证: .
.
已知圆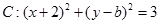
 过点
过点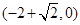 , 直线
, 直线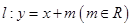 .
.
(1)求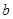 的值;
的值;
(2)若直线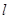 与圆C相切,求
与圆C相切,求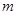 的值;
的值;
(3)若直线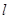 与圆C相交于M、N两点,且
与圆C相交于M、N两点,且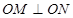 (O为原点),求实数
(O为原点),求实数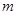 的值.
的值.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC, E为PC的中点,AD=CD=1,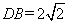 .
.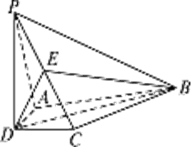
(1)证明:PA∥平面BDE;
(2)证明:AC⊥平面PBD;
(3)求直线BC与平面PBD所成的角的正切值.
如图,PA⊥平面ABC, 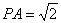 , AB=1,
, AB=1,  , AC=2.
, AC=2.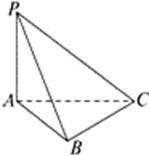
(1)求证: BC⊥平面PAB;
(2)求二面角B-PA-C的大小.
已知函数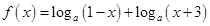 ,其中
,其中 .
.
(1)求函数f (x)的定义域:
(2)若函数f (x)的最小值为-4,求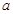 的值。
的值。
已知函数 (其中
(其中 为常数,
为常数, )的图象过点,
)的图象过点, .
.
(1)求
(2)若不等式 在
在 时恒成立,求
时恒成立,求 的取值范围.
的取值范围.