如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC, E为PC的中点,AD=CD=1,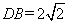 .
.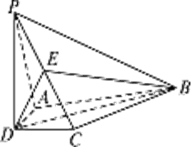
(1)证明:PA∥平面BDE;
(2)证明:AC⊥平面PBD;
(3)求直线BC与平面PBD所成的角的正切值.
如图,已知抛物线 , 点 , 抛物线上的点
过点 作直线 的垂线,垂足为 .
( I ) 求直线 斜率的取值范围;
( II ) 求 的最大值。

已知函数 .
( I ) 求 的导函数;
( II ) 求 在区间 上的取值范围.
如图,已知四棱锥 是以 为斜边的等腰直角三角形, , 为 的中点.
(I ) 证明: 平面 ;
( II )求直线 与平面 所成角的正弦值.

已知函数 .
( I ) 求 的值;
( II )求 的最小正周期及单调递增区间;
, 则称 是数列 的一个 " 时刻" 记 是数列 的所有 " 时刻" 组成的集合.
(1)对数列 A: , 写出 的所有元素;
(2)证明:若数列 中存在 使得 , 则 ;
(3)证明:若数列 满足 则G(A)的元素个数小于 ;