, 则称 是数列 的一个 " 时刻" 记 是数列 的所有 " 时刻" 组成的集合.
(1)对数列 A: , 写出 的所有元素;
(2)证明:若数列 中存在 使得 , 则 ;
(3)证明:若数列 满足 则G(A)的元素个数小于 ;
某校100位学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是: 、
、 、
、 、
、 、
、 .
.
(Ⅰ)求图中 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生的语文成绩某些分数段的人数( )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数( )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在 之外的人数.
之外的人数.
| 分数段 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 |
频数 |
频率 |
| 145.5~149.5 |
1 |
0.02 |
| 149.5~153.5 |
4 |
0.08 |
| 153.5~157.5 |
20 |
0.40 |
| 157.5~161.5 |
15 |
0.30 |
| 161.5~165.5 |
8 |
0.16 |
| 165.5~169.5 |
m |
n |
| 合 计 |
M |
N |
(1)求出表中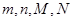 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?
甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的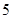 次预赛成绩记录如下:甲:
次预赛成绩记录如下:甲: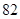 ,
,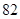 ,
,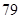 ,
,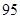 ,
,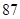 乙:
乙: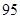 ,
,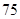 ,
,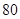 ,
,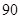 ,
,
(1)用茎叶图表示这两组数据;(2)求甲、乙两人的成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适说明理由?
写出计算1+2+3+…+100的值的算法语句.(要求用循环结构)
已知函数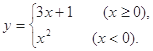 画出输入自变量
画出输入自变量 的值求函数值y的程序框图
的值求函数值y的程序框图