(本小题满分12分)
已知函数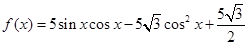 ,(Ⅰ)确定函数
,(Ⅰ)确定函数 的单调增区间;(Ⅱ)当函数
的单调增区间;(Ⅱ)当函数 取得最大值时,求自变量
取得最大值时,求自变量 的集合.
的集合.
已知双曲线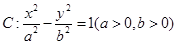 的离心率为
的离心率为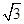 ,右准线方程为
,右准线方程为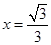 ,
,
(1)求双曲线C的方程;
(2)已知直线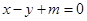 与双曲线C交于不同的两点A,B,且线段AB的中点在以双曲线C的实轴长为直径的圆上,求m的值.
与双曲线C交于不同的两点A,B,且线段AB的中点在以双曲线C的实轴长为直径的圆上,求m的值.
已知抛物线y2=-x与直线y=k(x+1)交于A、B两点.
(1)求证:OA⊥OB;
(2)当DAOB的面积等于 时,求k的值.
时,求k的值.
在直角坐标系中, 为坐标原点,如果一个椭圆经过点P(3,
为坐标原点,如果一个椭圆经过点P(3, ),且以点F(2,0)为它的一个焦点.
),且以点F(2,0)为它的一个焦点.
(1)求此椭圆的标准方程;
(2)在(1)中求过点F(2,0)的弦AB的中点M的轨迹方程.
设椭圆 的左焦点为
的左焦点为 ,离心率为
,离心率为 ,过点
,过点 且与
且与 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为
(1)求椭圆方程;
(2)过点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,当
,当 面积最大时,求
面积最大时,求
已知抛物线 ,
, 为坐标原点,动直线
为坐标原点,动直线 与
与
抛物线 交于不同两点
交于不同两点
(1)求证: ·
· 为常数;
为常数;
(2)求满足 的点
的点 的轨迹方程。
的轨迹方程。