已知函数 .
( I ) 求 的值;
( II )求 的最小正周期及单调递增区间;
如图,正方形ABCD和三角形ACE所在的平面互相垂直.EF∥BD,AB= EF.求证:
EF.求证:
(1)BF∥平面ACE;
(2)BF⊥BD.
在如图所示的多面体中,已知正三棱柱ABCA1B1C1的所有棱长均为2,四边形ABDC是菱形.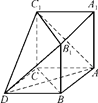
(1)求证:平面ADC1⊥平面BCC1B1;
(2)求该多面体的体积.
如图,在直四棱柱ABCDA1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,且AB=2CD,在棱AB上是否存在一点F,使平面C1CF∥平面ADD1A1?若存在,求点F的位置;若不存在,请说明理由.
如图①,在等腰梯形ABCD中,AD∥BC,AB=AD,∠ABC=60°,E是BC的中点.如图②,将△ABE沿AE折起,使二面角BAEC成直二面角,连结BC、BD,F是CD的中点,P是棱BC的中点.求证:
图①图②
(1)AE⊥BD;
(2)平面PEF⊥平面AECD.
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,G、H分别为DC、BC的中点.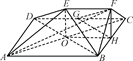
(1)求证:平面FGH∥平面BDE;
(2)求证:平面ACF⊥平面BDE.