如图,四边形ABCD中,点E在边CD上,连结AE、BE.给出下列五个关系式:①AD∥BC;②DE=CE;③∠1=∠2;④∠3=∠4;⑤AD+BC=AB.将其中的三个关系式作为题设,另外两个作为结论,构成一个命题.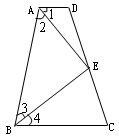
⑴用序号写出一个真命题(书写形式如:如果×××,那么××);并给出证明;
⑵用序号再写出三个真命题(不要求证明)
(本小题满分7分)
“保护环境,人人有责”,为了了解某市的空气质量情况,某校环保兴趣小组,随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)估计该市这一年(365天)空气质量达到“优”和“良”的总天数;
(3)计算随机选取这一年内的某一天,空气质量是“优”的概率.
2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题: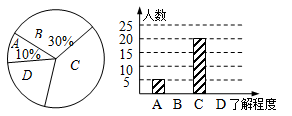
(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
(1)已知m是方程 的一个根,求
的一个根,求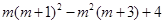 的值;
的值;
(2)一次函数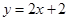 与反比例函数
与反比例函数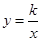 (
( )的图象都经过点A(1,m),
)的图象都经过点A(1,m),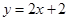 的图象与x轴交于点B.
的图象与x轴交于点B.
①求点B的坐标及反比例函数的表达式;
②点C(0,﹣2),若四边形ABCD是平行四边形,请在直角坐标系内画出▱ABCD,直接写出点D的坐标,并判断D点是否在此反比例函数的图象上,并说明理由.
如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.
(本小题满分10分)
如图隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用 表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为
表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为 m。
m。
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱璧上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?