为了解学生的身高情况，抽测了某校17岁的50名男生的身高.数-优题课

为了解学生的身高情况，抽测了某校17岁的50名男生的身高.数据如下（单位：米）：

身高	1.57	1.59	1.60	1.62	1.63	1.64	1.65	1.66	1.68
人数	1	1	2	2	3	2	1	6	5
身高	1.69	1.70	1.71	1.72	1.73	1.74	1.75	1.76	1.77
人数	8	7	2	3	2	1	2	1	1

若将数据分成7组，取组距为0.03米，相应的频率分布表是：

分组	频数	频率
1.565~1.595	2	0.04
1.595~1.625	4	0.08
1.625~1.655	6	0.12
1.655~1.685	11	0.22
1.685~1.715	17	0.34
1.715~1.745	6	0.12
1.745~1.775	4	0.08
合计	50	1

请回答下列问题：
（1）样本数据中，17岁男生身高的众数、中位数分别是多少？
（2）依据样本数据，估计这所学校17岁的男生中，身高不低于1.65米且不高于1.70米的学生所占的百分比；
（3）观察频率分布表，指出该校17岁的男生中，身高在哪个数据范围内的频率最大.如果该校17岁的男生共有350人，那么在这个身高范围内的人数估计有多少人？

科目数学题型解答题难度中等

如图1，经过原点 $O$ 的抛物线 $y = a x^{2} + bx (a$ 、 $b$ 为常数， $a \neq 0)$ 与 $x$ 轴相交于另一点 $A (3, 0)$ ．直线 $l : y = x$ 在第一象限内和此抛物线相交于点 $B (5, t)$ ，与抛物线的对称轴相交于点 $C$ ．

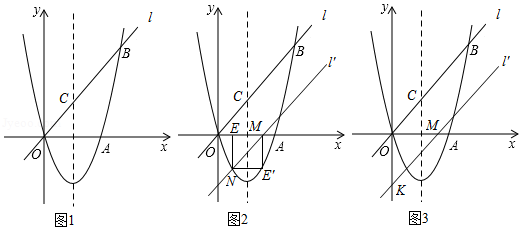
（1）求抛物线的解析式；

（2）在 $x$ 轴上找一点 $P$ ，使以点 $P$ 、 $O$ 、 $C$ 为顶点的三角形与以点 $A$ 、 $O$ 、 $B$ 为顶点的三角形相似，求满足条件的点 $P$ 的坐标；

（3）直线 $l$ 沿着 $x$ 轴向右平移得到直线 $l'$ ， $l'$ 与线段 $OA$ 相交于点 $M$ ，与 $x$ 轴下方的抛物线相交于点 $N$ ，过点 $N$ 作 $NE ⊥ x$ 轴于点 $E$ ．把 $ΔMEN$ 沿直线 $l'$ 折叠，当点 $E'$ 恰好落在抛物线上时（图 $2)$ ，求直线 $l'$ 的解析式；

（4）在（3）问的条件下（图 $3)$ ，直线 $l'$ 与 $y$ 轴相交于点 $K$ ，把 $ΔMOK$ 绕点 $O$ 顺时针旋转 $90 °$ 得到△ $M' OK'$ ，点 $F$ 为直线 $l'$ 上的动点．当△ $M^{'} FK'$ 为等腰三角形时，求满足条件的点 $F$ 的坐标．

某商店销售 $A$ 型和 $B$ 型两种电脑，其中 $A$ 型电脑每台的利润为400元， $B$ 型电脑每台的利润为500元．该商店计划再一次性购进两种型号的电脑共100台，其中 $B$ 型电脑的进货量不超过 $A$ 型电脑的2倍，设购进 $A$ 型电脑 $x$ 台，这100台电脑的销售总利润为 $y$ 元．

（1）求 $y$ 关于 $x$ 的函数关系式；

（2）该商店购进 $A$ 型、 $B$ 型电脑各多少台，才能使销售总利润最大，最大利润是多少？

（3）实际进货时，厂家对 $A$ 型电脑出厂价下调 $a (0 < a < 200)$ 元，且限定商店最多购进 $A$ 型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑销售总利润最大的进货方案．

反比例函数 $y = \frac{k}{x} (k$ 为常数，且 $k \neq 0)$ 的图象经过点 $A (1, 3)$ 、 $B (3, m)$ ．

（1）求反比例函数的解析式及 $B$ 点的坐标；

（2）在 $x$ 轴上找一点 $P$ ，使 $PA + PB$ 的值最小，求满足条件的点 $P$ 的坐标．

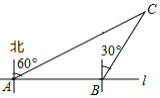
如图，某市郊外景区内一条笔直的公路 $l$ 经过 $A$ 、 $B$ 两个景点，景区管委会又开发了风景优美的景点 $C$ ．经测量， $C$ 位于 $A$ 的北偏东 $60 °$ 的方向上， $C$ 位于 $B$ 的北偏东 $30 °$ 的方向上，且 $AB = 10 km$ ．

（1）求景点 $B$ 与 $C$ 的距离；

（2）为了方便游客到景点 $C$ 游玩，景区管委会准备由景点 $C$ 向公路 $l$ 修一条距离最短的公路，不考虑其他因素，求出这条最短公路的长．（结果保留根号）

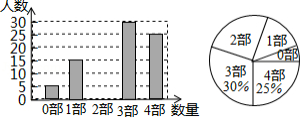
中华文化源远流长，在文学方面，《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”．某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题在全校学生中抽取 $n$ 名学生进行调查．根据调查结果绘制成如图所示的两个不完整的统计图，请结合图中信息解决下列问题：

（1）求 $n$ 的值；

（2）请将条形统计图补充完整；

（3）若该校共有2000名学生，请估计该校四大古典名著均已读完的人数．