为了配合“八荣入耻”宣传教育,针对闯红灯现象时有发生的实际情况,八年级某班开展了一次题为“红灯与绿灯”的课题学习活动,他们将全班学生分成8个小组,其中第①~⑥组分别负责早、中、晚三个时段闯红灯违章现象的调查;第⑦小组负责查阅有关红绿灯的交通法则,第⑧小组负责收集有关的交通标志,数据汇总如下表所示,并作了车辆(行人)违章的频数条形统计图.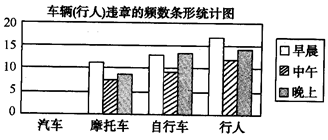
部分时段车流量情况调查表
| |
负责组别 |
车流总量 |
每分钟车流量 |
| 早晨上学6:00~7:00 |
①② |
2747 |
92 |
| 中午放学11:20~11:50 |
③④ |
1449 |
48 |
| 下午放学5:00~5:30 |
⑤⑥ |
3669 |
122 |
回答下列问题:
(1)写出2条交通法则:①_________;②________;
(2)在下面的方框内,画出2枚交通标志示意图,并说明标志的含义.
(3)早晨、中午、晚上三个时段每分钟车流量的极差是______,这三个时段的车流总量的中位数是_______.
(4)观察表中的数据及条形统计图,写出发现的一种现象并分析其产生的原因.
(5)通过以上调查、统计、分析,向交通管理部门提一条合理化建议.
△ABC的外角∠CBD,∠BCE的角平分线交于点F,求证AF平分∠BAC.
如图,P为∠AOB内一点,OA=OB,且△OPA与△OPB面积相等,求证∠AOP=∠BOP.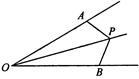
古代有一位商人有一块三角形土地,土地的一边靠水渠,如图所示,现在他想把这块土地平均分给他的三个儿子,为使土地灌溉方便,想使每个儿子分得的土地都有一边和水渠相邻.试问应如何分割这块土地?请你说明理由。
如图,在△ABC中,若AD是BC边上的中线,则有BD == ,若过A点作BC边上的高AE,利用三角形的面积公式可求得S△ABD==
,若过A点作BC边上的高AE,利用三角形的面积公式可求得S△ABD== S△ABC,请你任意画一个三角形,将这个三角形的面积四等分。
S△ABC,请你任意画一个三角形,将这个三角形的面积四等分。
多边形的木架具有不稳定性,但钉一些木条可使其形状不变。
(1)
| 多边形的边数 |
4 |
5 |
6 |
7 |
| 至少要钉木条根数 |
(2)根据上面规律要使一个n边形(n≥4)的形状不变,至少要钉几根木条?